基準との差を使った平均の求め方 平均 = 基準との差の合計 個数(人数) 基準の値 表は生徒5人のテストの得点と、その得点の基準との差を正負の数で表してある。 総務 36協定は結んでいて、1年単位の変形労働協定書は結んでいません。1週間の平均労働時間数をどのように算出すれば良いのか、計算式などがあれば教えて下さい。 結んでいない場合の、1週間の平均労働時間数の考え方が知りたいです。 1年単位の変形労働振り子が1往復する時間を複数の児童ではか る。 平均の求め方について学習する。 グループの中で役割分担をする。 ストップウォッチの使い方を練習する。 実験結果から,振り子が1往復する時間に関 係する条件を発表する。 まとめをする。

10分で分かる 平均賃金の計算方法
中1 数学 平均の求め方
中1 数学 平均の求め方-アで求めた日別平年値を用いて、1 月1 日から12 月31 日まで、9 日間移動平均値(d1_1~d365_1)を求める。 平均した値は、その中日の値とする。 例えば、1 月1 日から1 月9 日までの資料による値は、1 月5 日の値とする。 実際に、空気1 mol当たりの重さ(=平均分子量)を求めてみましょう。 "mol"とは個数の単位ですから、40 molは4(×60×10^23)個、10 molは1(×60×10^23)個と仮に考えます。



流量の公式は 1分でわかる公式 流量計算 平均流速との関係
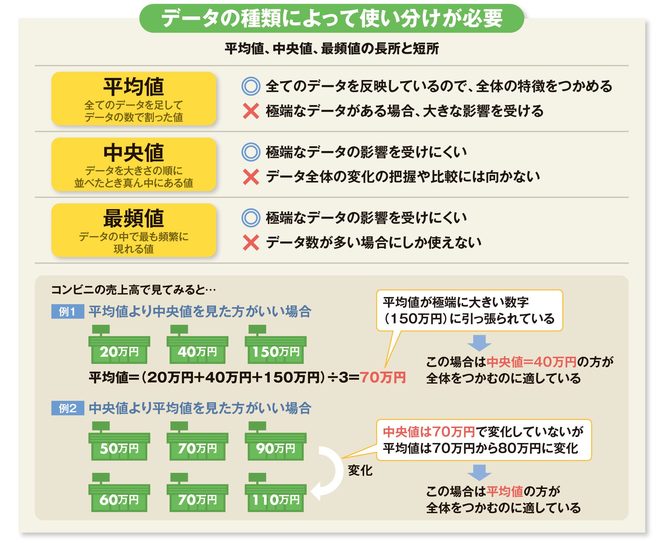
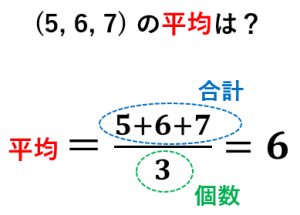
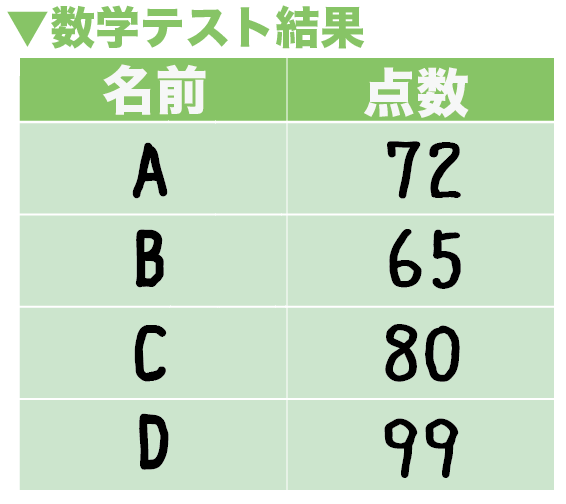
「平均値」は、すべてのデータを たし算 して、全体の 10で割れば 求められるね。 「中央値」は、真ん中の人の値だよね。10人のうちの真ん中はどこ? 5番目と6番目の人の間だね。5番目と6番目の人の値は1000円だから、これが中央値になるよ。中1数学『資料の整理と分析』のところでの平均値の求め方は2パターンです。 一つは小学校のときからのおなじみの平均値の求め方です。 平均値: 個々の資料の値の合計を資料の総数で割った値 もう一つが、度数分布表から平均値を求める求め方です。\(平均値=資料の値の合計÷資料の個数\) となります。 例 生徒 \(8\) 人のある数学のテストの得点(点) \(42 , 55 , 72 , 80 , 62 , 75 , 90 ,65 \) \(8\) 人の、この数学のテストの平均点を求めます。 \(8\) 人の平均点
中1数学単元テスト 仮の平均の求め方 解答・解説です。 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new新しい 度数分布表 平均値 求め方 ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手 度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを このような平均の求め方は常に利用できるが,\ 常に効果的とは限らない 各値のばらつきが大きい場合(129,\ 223,\ 528,\ 3,\ 609)は差を求めること自体が面倒である 正負の数を利用した計算の工夫、仮平均を利用した平均(中1) 文字式の表し方(積・商
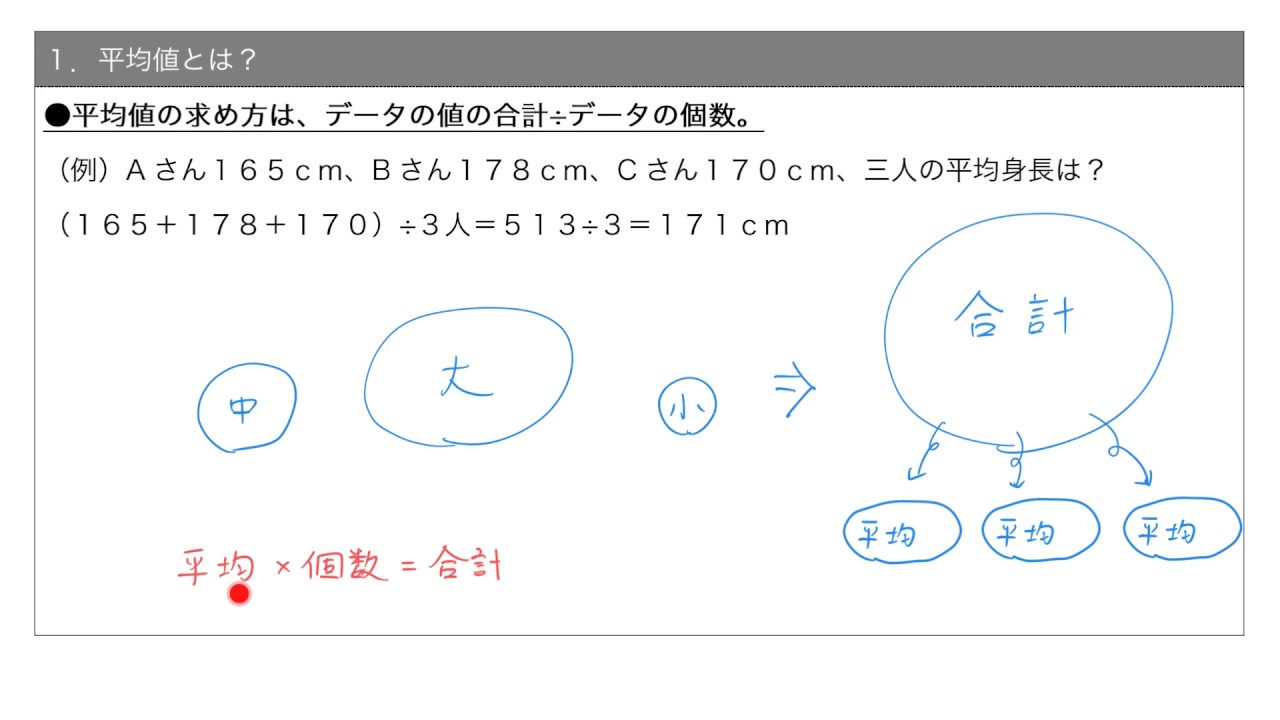
平均=仮平均+差の平均 魔方陣 「たて」「横」「斜め」で 求められるところを見つける かずのかず 以上、「数学嫌いな人が、 数学を楽しく好きになって欲しい」 かずのかずでした 中1数学「正負の数の乗法 除法」の問題 どこよりも簡単な解き方・求め 平均値の求め方は ①:データをすべて足す ②:①で求めた値をデータの個数で割る でしたね。 よって、求める平均値は ()÷4 = 166(cm)・・・(答) となります。子供の平均身長と平均体重 身長・体重の全国平均 (18年公開の総務省データ)と比較します。 ※計算結果や情報等に関して当サイトは一切責任を負いません。 また個別相談は対応しません。




正の数 負の数の応用 中学一年生 クラス授業 海星学院 泉校 京都府八幡市男山泉3 21




平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ
上の公式において,平均演算子「E」は,期待値 Expectation の頭文字からきているものです。上の式の中で,2つ目の公式が統計ではよく用いられます。覚えておいた方がよいでしょう。 一度に,理解できなくてもかまいません。高校数学 対数log Abの近似値求め方 評価の方法 受験の月 度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを次の図は,1組の男子16人と2組の男子15人の記録をそれぞれヒストグラムに表したものである。 下の(1),(2)に答えなさい。 (1) 上の1組と2組のヒストグラムを比較した内容として適切なものを,下のア~オの中からすべて選び,その記号をかきかさい。
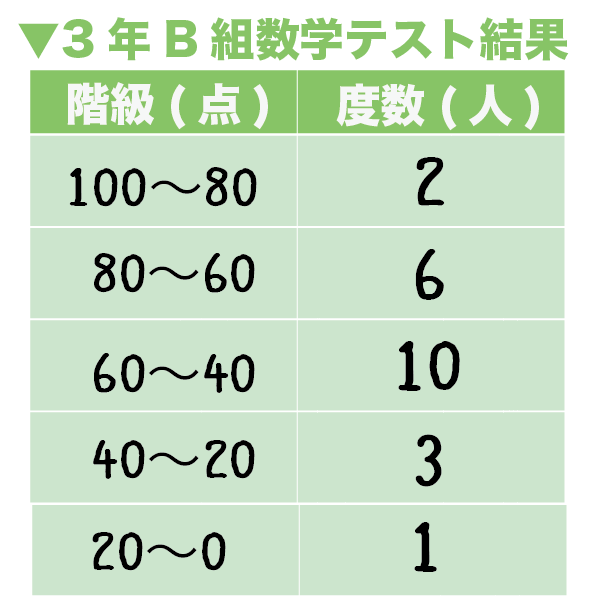



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



分散とは 公式 求め方や計算問題 分散分析 多重比較の意味も 受験辞典
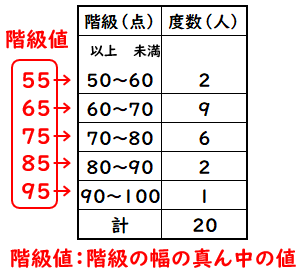
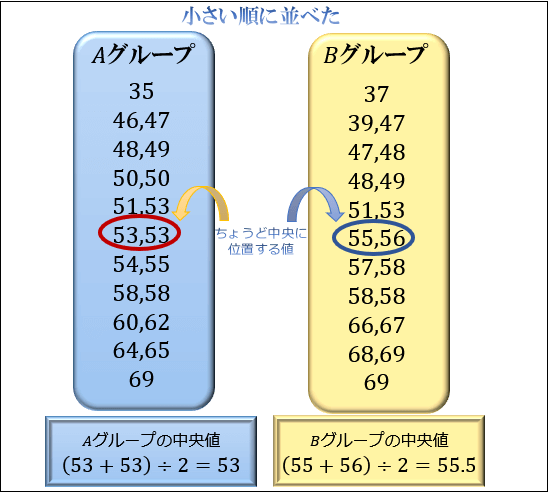
平均値,中央値,最頻値の求め方といくつかの例 データ群の特徴を一つの数値で表したものを代表値と呼ぶ。 代表値の中でも平均値,中央値,最頻値が有名。 平均値,中央値,最頻値の意味と計算方法を解説します。 いくつかの具体例を通じて1平均(平均値)ふつうは,平均といいます。 資料の散らばりのとらえ方の最も素朴な方法は,資料を1つの数直線の上に並べてみることです。 このようにすると,散らばりのようすや集団の中における個々の位置がとらえやすくなります。それらの平均の値を中央値とします。 データの値が偶数個で、真ん中に位置する値を見つけれない場合には、 このように真ん中ラインを挟む2つのデータを見ることで中央値を求めていきましょう。 中央値は何番目? (偶数) 今回のようにデータが4個ある場合には、 2番目と3番目の平均を取れば良いということでしたが、 もしも、データが100個ある場合には




平均算を小学生に教えるための分かりやすい解説 問題の解き方 数学fun




平均値の求め方 基本問題から階級値 相対度数を用いた応用問題の解き方
クラス平均と個人平均 データの読込 成績データ seisekixls を機械可読データ形式に保存しなおして(カンマ区切りのcsv形式が代表的)、これを読み込む。 以下の例では、Windows環境 Z/R/data 内に、csv形式で seisekicsv として保存したとしている(自分用に適宜解釈し直すこと)。考え方 45 cm 以上 50 cm 未満の階級値 47 5 cm を仮の平均とする。 平均値=仮の平均+ {(階級値-仮の平均)×(度数)}の合計正負の数の利用 ~平均の求め方~ テーマ: ├勉強法:数学(中1) 下の表は5人の生徒の身長を150cmを基準にして、その数より高い場合を正の数、低い場合を負の数で表したものです。 5人の生徒の身長の平均を求めなさい。 この数字は150cmを基準にして、どれだけ高いか低いかを表しています。 つまり、Aは152cm、Bは161cm、Cは146cm、Dは158cmそしてEは




中1 数学 中1 87 代表値と散らばり Youtube




度数分布表から平均値と最頻値を求める 苦手な数学を簡単に
平均値は、$\overline{x} = \frac{1}{10} () = 5$より求まります。 平均値についてはかなりとっかかりやすいと思うのでサクサク進みます! 平均値のメリット、デメリット 平均値のメリットとしては、すべての値が反映されるということです。ある数の何パーセントはいくつ? ある数の パーセントはいくつなのか計算出来ます。 ※ 例えばある学校の全体の生徒数800人の内、女子生徒が43%だとして、それは何人なのか計算出来ます。「平均値」は、すべてのデータを たし算 して、全体の 12で割れば 求められるね。 「中央値」は、真ん中の人の値だよ。12人のうちの真ん中だから、6番目と7番目の人の間。6番目と7番目の人の値を足して2で割れば「中央値」が出せるね。



Search Q E5 B9 E5 9d 87 E5 80 E6 B1 81 E6 96 B9 E7 B0 A1 E5 8d 98 Tbm Isch



流量の公式は 1分でわかる公式 流量計算 平均流速との関係
これらの観測値の平均\(\overline{x}\)というのは次の式で表されます。 $$\overline{x} = \frac{1}{n}(x_1x_2x_n) = \frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } x_i$$ 平均≒重心 平均は、観測値データの重心を表す指標として使われることが多いです。 答えが (x4)06(x3)04=722 の式が書いてあったのですが、平均の出し方は (平均 ︎人数 平均 ︎人数) 全体の人数 ではないのですか? なぜ全体の人数で割らないのか教えてくこの求め方から、求め方を導く。 (平均×人数+得点×1人)÷(人数+1) =(平均×人数+(平均+差))÷(人数+1) =(平均×(人数+1))+差)÷(人数+1) =平均+(差÷(人数+1))




小学校5年 算数 平均の表し方 Youtube




偏差値とは何 偏差値の意味と求め方 計算方法をわかりやすく解説 栄光の個別ビザビ 個別指導の塾 学習塾なら
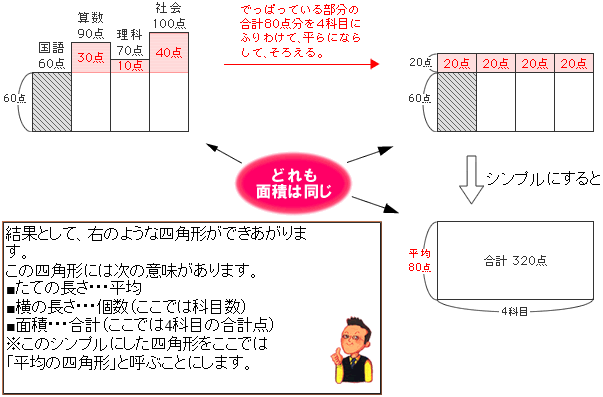



平均算 算数の教え上手 学びの場 Com




標本平均と標本分散とは 具体例と性質 証明付 理数アラカルト




理科の平均の速さはどうやって求めますか Clear



中学数学 平均の求め方 数学について質問します 問題文1 Yahoo 知恵袋
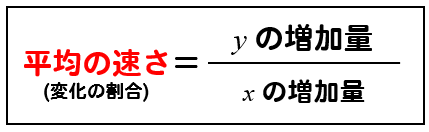



中3 数学 平均の速さの求め方を解説 数スタ
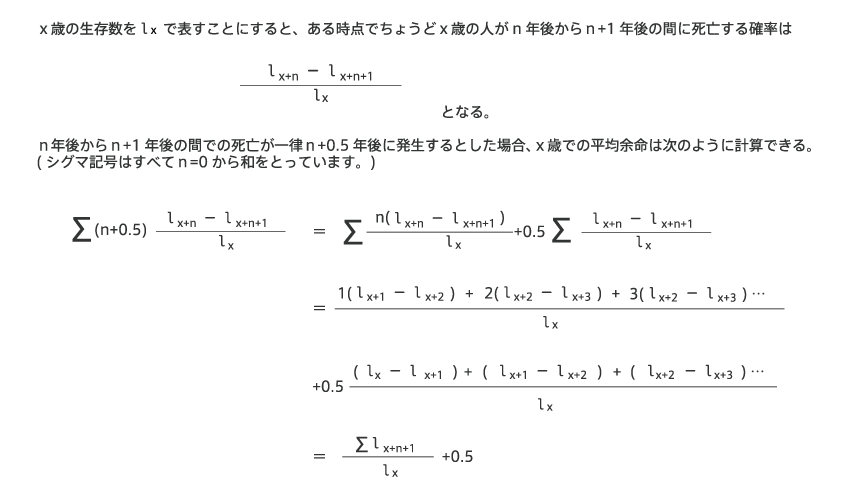



平均余命はどう計算されているか Pmas Iicパートナーズ
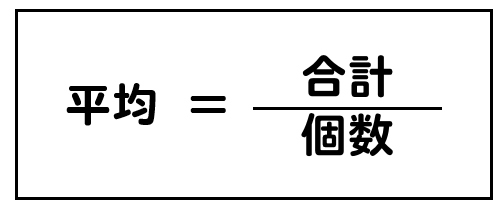



中1数学 平均を文字式で表す問題を解説 数スタ
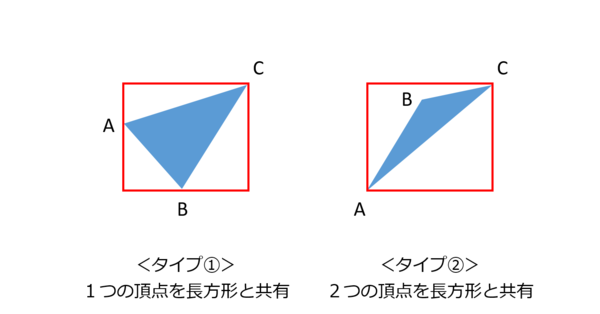



正方形の中にある三角形の面積の平均の求め方 Excelで答え合わせ Musyokutoumei
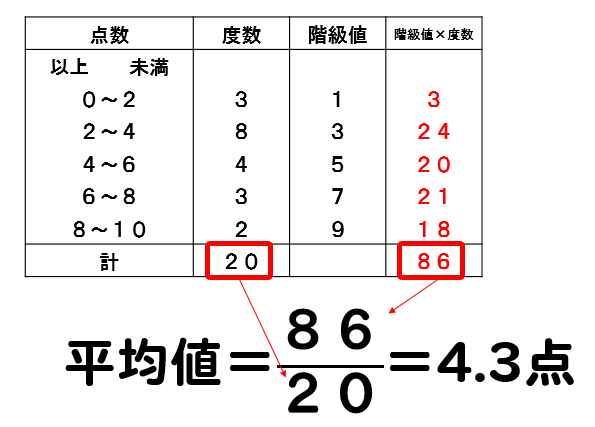



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




代表値 平均値 中央値 最頻値 の意味と違い 数学fun



データの分析を総まとめ 公式の覚え方や裏ワザ 重要記事一覧 受験辞典
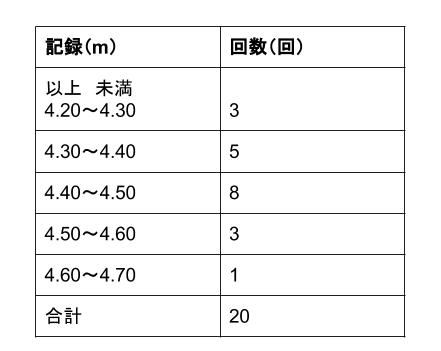



中学数学 代表値 平均値 中学数学の無料オンライン学習サイトchu Su



中1の正負の数を使った平均の求め方についての問題 この画像の 3 Yahoo 知恵袋




小6 算数 小6 35 平均とちらばり Youtube
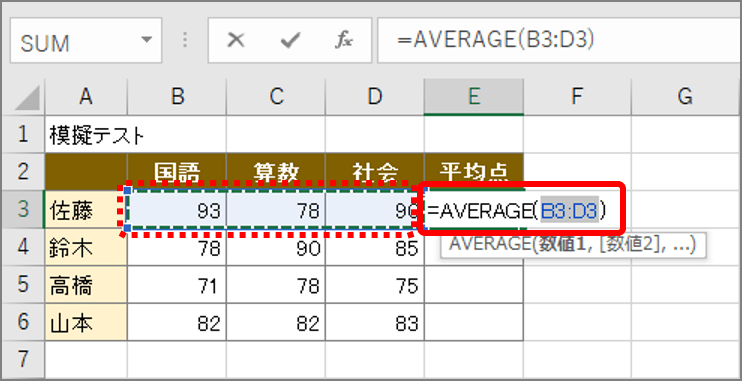



エクセル 平均 を簡単に求めよう いまさら聞けない平均算出ワザ3選 Getnavi Web ゲットナビ




高校数学 分散 とは 練習編 映像授業のtry It トライイット




平均値の求め方を教えて下さい Clear



32 3 移動平均 統計学の時間 統計web



中学数学 平均の求め方 数学について質問します 問題文1 Yahoo 知恵袋




中1数学 平均点の求め方 Youtube



小5算数の宿題 仮の平均 を使って平均を求める方法 がんばるブラザーズ



代表値 平均値 中央値 最頻値 の意味と違い 数学fun



世界四季報 Sur Twitter 中1数学 資料の活用 中央値の求め方 Youtube T Co Ccfwdf7bgp 中央値の求め方の記憶がすっぽり抜けていたんだけど習っていなかったのかな
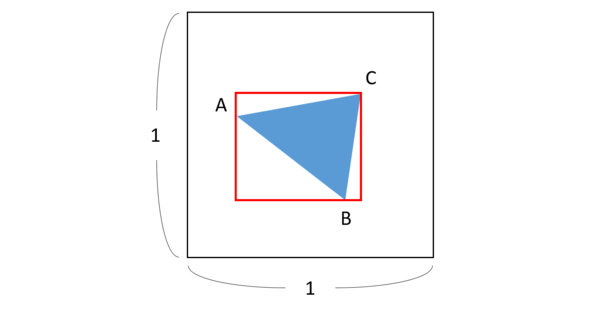



正方形の中にある三角形の面積の平均の求め方 三角形を囲む長方形の面積 Musyokutoumei




平均算を小学生に教えるための分かりやすい解説 問題の解き方 数学fun



平均の求め方 計算式 と意味 欠点 具体例で学ぶ数学




中1数学 数学のlim先生



要点 平均値と仮平均 Youtube




中学数学1年 正負の数を利用した計算の工夫 仮平均を利用した平均 受験の月




10分で分かる 平均賃金の計算方法




往復の平均の速さ 間違えずに求められますか



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




小5算数の宿題 仮の平均 を使って平均を求める方法 がんばるブラザーズ



3つの代表値 平均値 中央値 最頻値の使い分け データの代表はどれが最適 アタリマエ
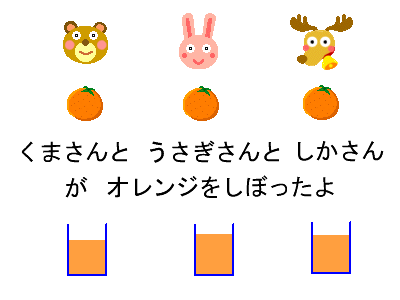



5年算数平均 教え方のポイント



無料 中1数学 標準問題 問題プリント 129 比例と反比例2 変域 式の求め方
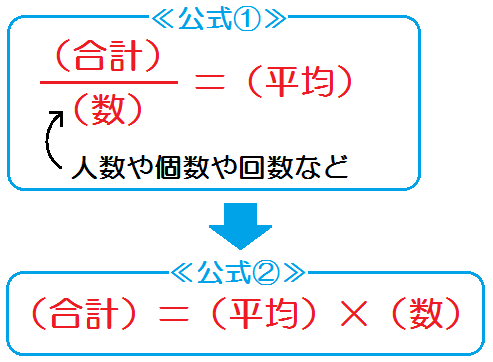



中学数学 1次方程式 文章題の解き方 平均



中学生向け 偏差値の求め方 出し方 簡単な計算方法
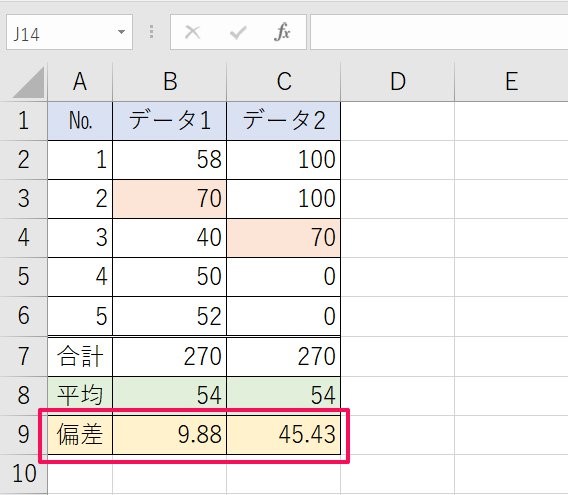



Excel応用編 関数で標準偏差を求めるには 関数を使って求めてみよう ワカルニ
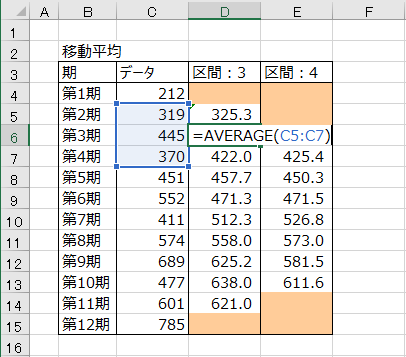



移動平均の計算方法 ブログ 統計web




資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト



4gr2ad9qt6s Com E5 86 E6 95 A3




中1数学 平均値 と 中央値 例題編 映像授業のtry It トライイット




センター試験頻出 分散とは 求め方や意味を徹底解説 高校生向け受験応援メディア 受験のミカタ




中1数学 平均を文字式で表す問題を解説 数スタ
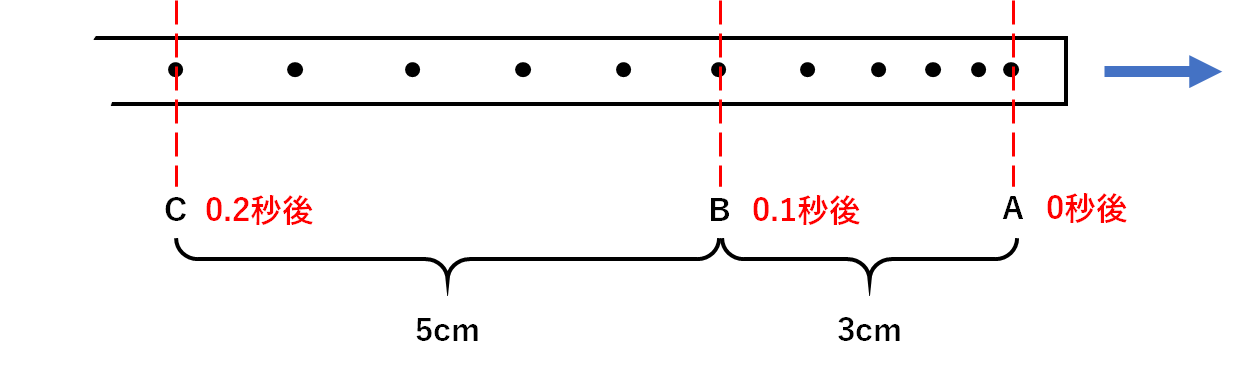



中3物理 瞬間の速さ 中学理科 ポイントまとめと整理



中学校理科の公式一覧




平均の求め方 小学生で学ぶ公式は 問題の解き方を解説 中学数学 理科の学習まとめサイト




中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく



第六回 Average関数だけでは 平均値 の落とし穴にはまるかも 本当は怖いexcel エクセル の話
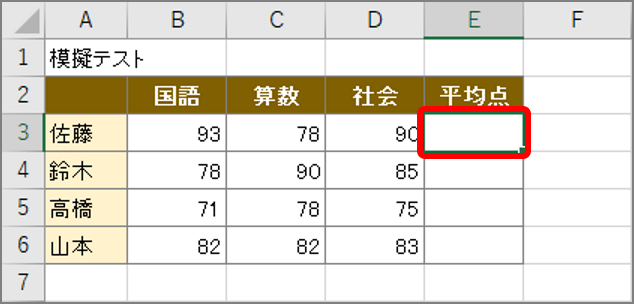



エクセル 平均 を簡単に求めよう いまさら聞けない平均算出ワザ3選 Getnavi Web ゲットナビ
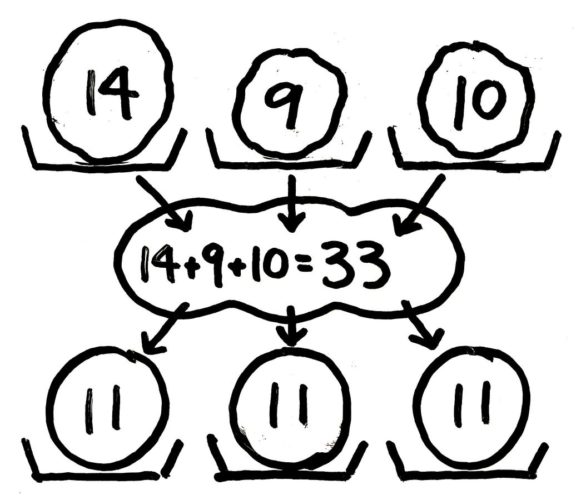



小学5 6年生 平均って何 求め方 問題の解き方をまとめました そうちゃ式 分かりやすい図解算数 別館



2
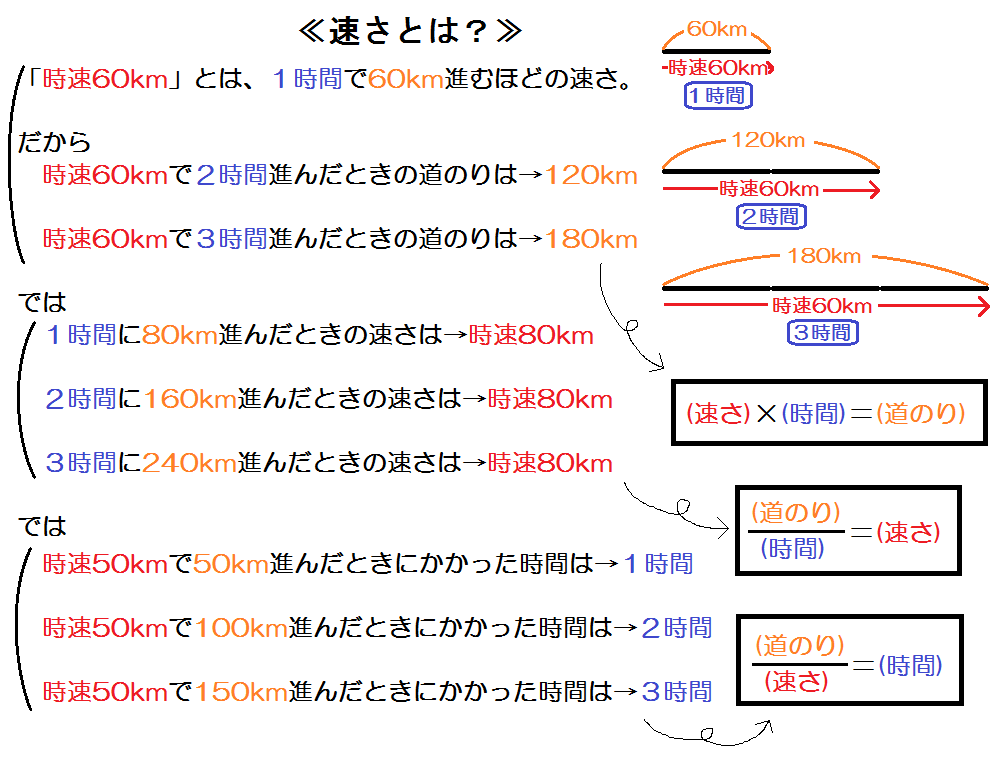



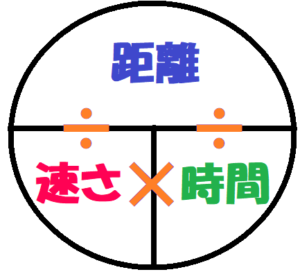
中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




数学 新 中1編 正負の数 中間試験対策 小4から始める高校受験 お母さん 一緒にがんばりましょう
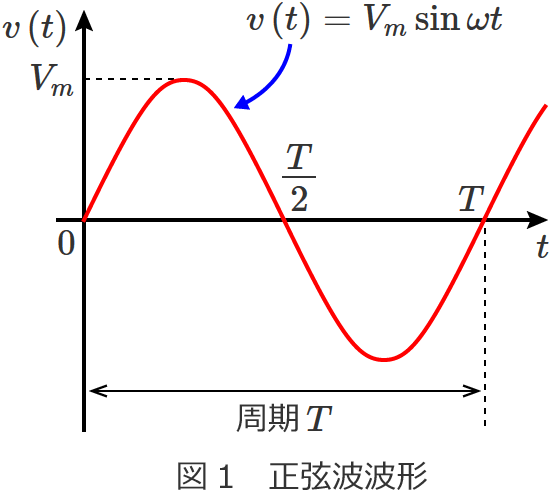



正弦波波形の実効値 平均値 最大値 波形率 波高率の計算方法




往復の平均の速さ 間違えずに求められますか




偏差値とは何か 図解でわかるその意味と使い道 求め方 アタリマエ
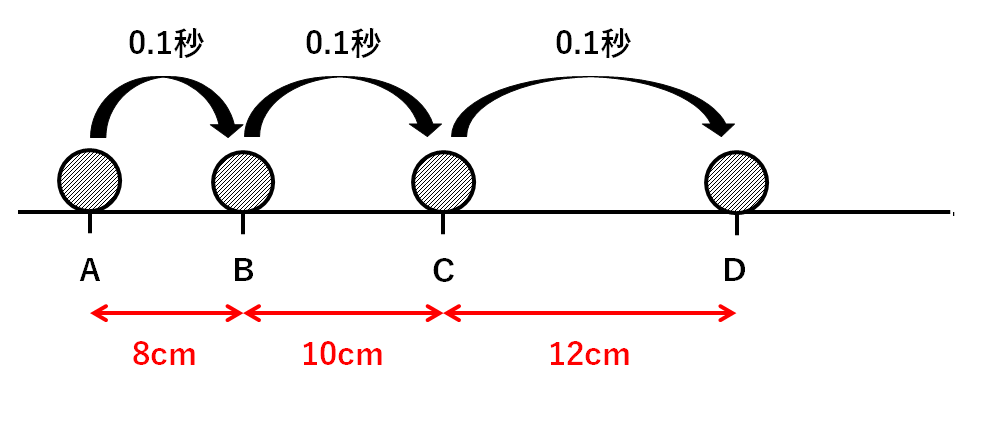



中3物理 速さ ストロボ写真 中学理科 ポイントまとめと整理




平均の求め方



3




度数分布表から平均値を求める 中学1年の数学 身勝手な主張



Q Tbn And9gct9g81v6fbuxe2zy40zobgjz7pv4jyf9dpik7xrlwfhfckmjg0k Usqp Cau
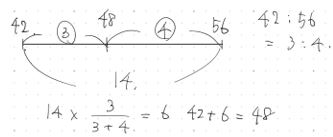



間違えやすい 平均の速さ を理解しよう 中学受験プロ講師ブログ




中1数学 平均値 と 中央値 例題編 映像授業のtry It トライイット
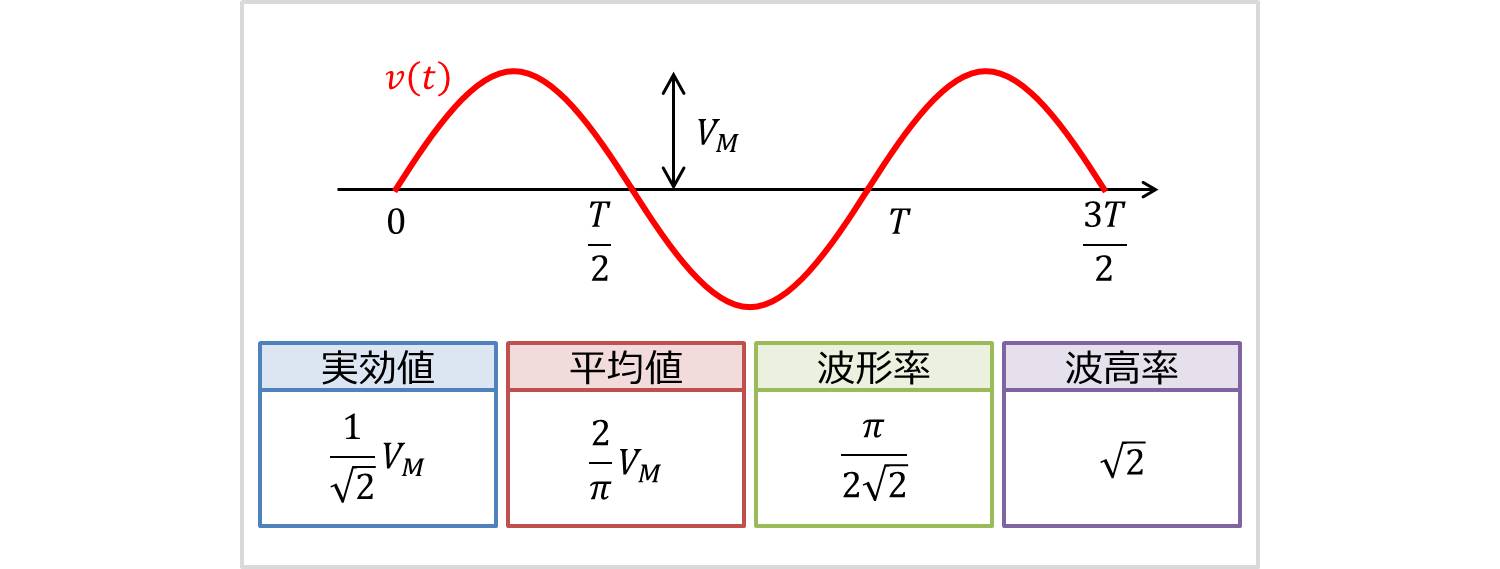



正弦波 の実効値 平均値 波形率 波高率の求め方 Electrical Information




平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ




中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく




平均の速度と瞬間の速度の違いとは 公式および求め方
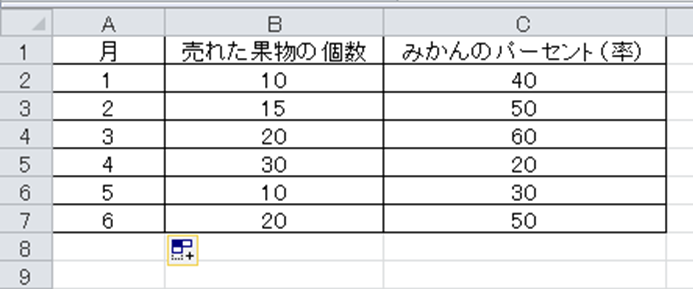



エクセルでパーセント 率 の平均を求める方法 上位のみの場合も More E Life




小5 算数 小5 21 平均 Youtube




小学校6年間で習う 算数の公式一覧 無料学習プリント 計算問題無料印刷 Origami Project



4gr2ad9qt6s Com E5 86 E6 95 A3




この問題の求め方教えてください 答えは イです Clear
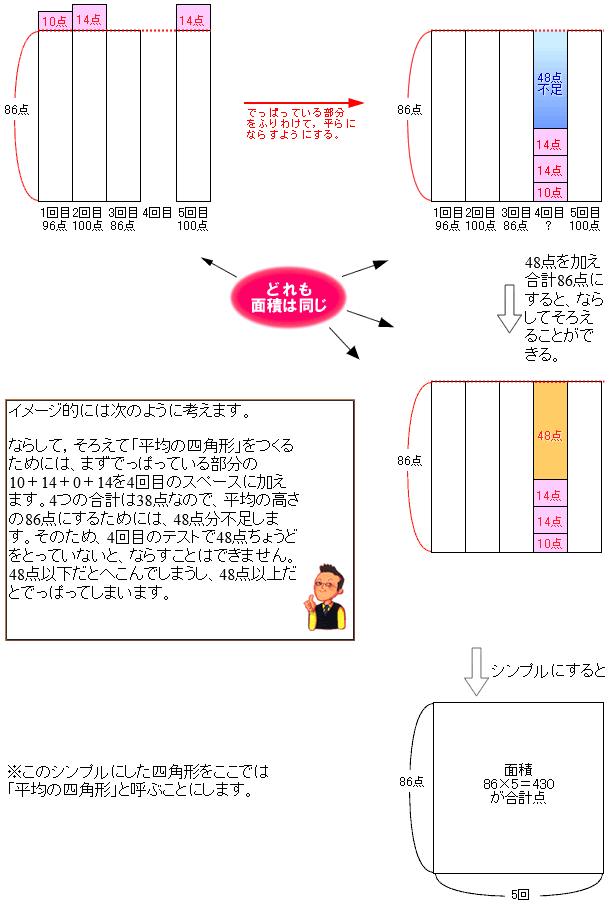



平均算 算数の教え上手 学びの場 Com




中学数学1年 代入と式の値 受験の月




中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく




平均の速度と瞬間の速度の違いとは 公式および求め方




小学5年生の算数 平均の求め方 練習問題プリント ちびむすドリル 小学生




Averageifs関数で複数の条件を指定して数値の平均を求める Excel関数 できるネット
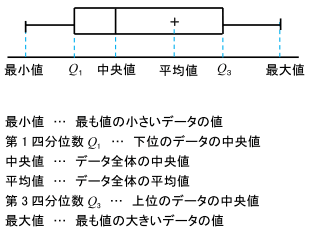



箱ひげ図のかき方 数学 苦手解決q A 進研ゼミ高校講座




標準偏差とは何か その求め方や公式の意味 使い方をわかりやすく説明します アタリマエ




5年算数平均 教え方のポイント




平均値 中央値 最頻値の求め方といくつかの例 高校数学の美しい物語




中1数学 表を使った平均 仮平均 の求め方のポイント Pikuu




正負の数の四則計算 分配法則 中学数学が好きになる



平均を求める関数 Average関数など の使い方 Excel関数




中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく



中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ




データの分析 平均値 中央値 最大値 最小値 範囲 最頻値



Q Tbn And9gcstvtcaabl2msd4sr2o1mkrqseey Gtjg97sl2qtthvxbinfwam Usqp Cau




度数分布表から平均値を求める 中学1年の数学 身勝手な主張



0 件のコメント:
コメントを投稿