最高点(v=0)までの所要時間t 0 は(54)=0から最高点の高さHは(56)でv=0から 質問4 速度vが初速度のn倍になる時間は,最高点までの時間t0 の何倍か。 (54)式から (1-n)倍 質問5 速度vが初速度のn倍になる高さはHの何倍か。(56)式から(1-n 2)倍 投げ下ろし 鉛直下方を正の向きにとる。相対性理論 速く動くと時間が遅れる アインシュタインの相対性理論において、有名なのが「高速で動くと時間が遅れる」という現象ですね。 これがどういうことなのか? ざっくり簡単に学んでいってみましょう。 時間の遅れと光の速度。 ちょと関係 Bさんは1時間あたり6km走った(時速6km) ⇒1時間あたりに進む距離が2km多いから、Aさんの方が速いね! 「速さ・時間・道のり」の三角関係 前置きが長くなりましたが、ここから「速さ・時間・道のりの公式」について具体的に考えていきましょう。

速度の計算と単位変換の教え方
速さと時間の関係
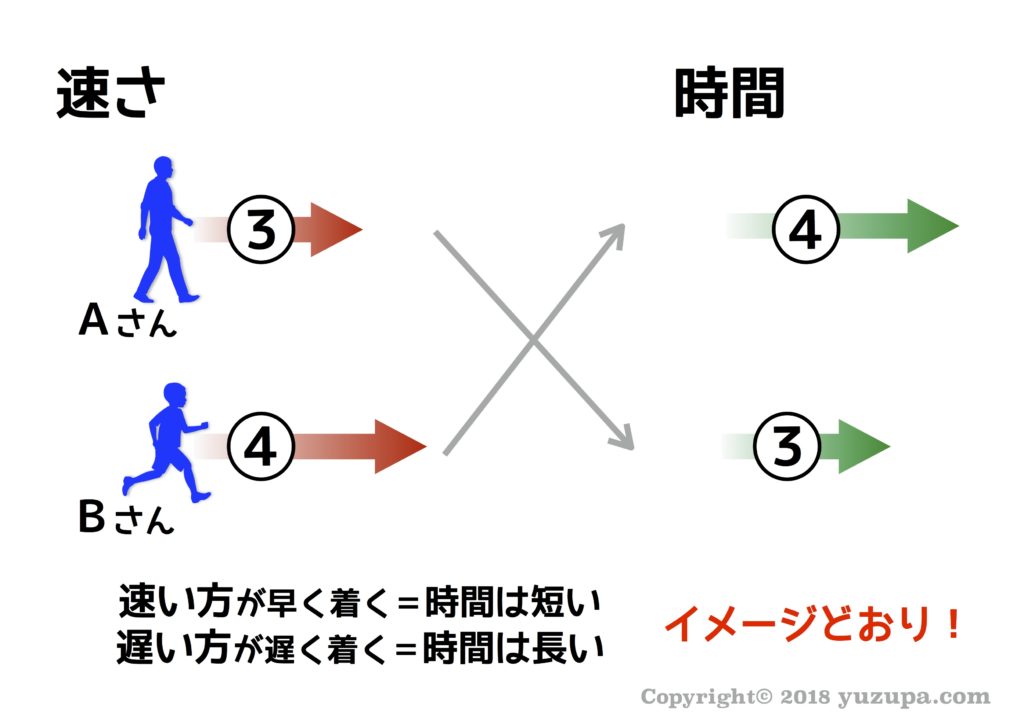
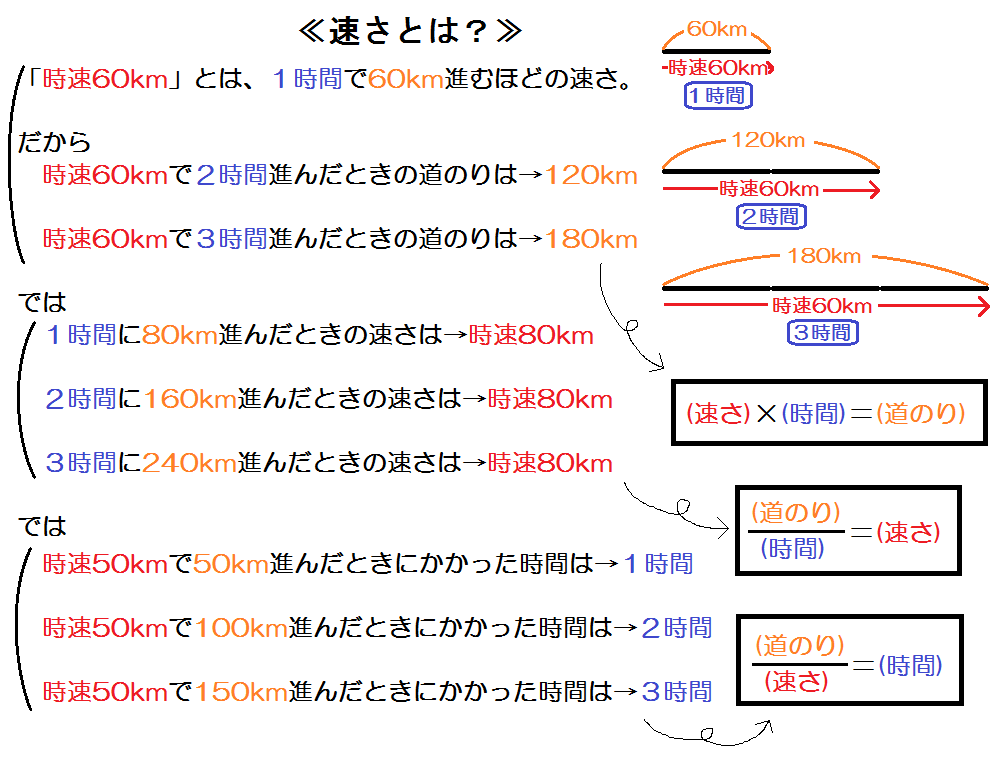
速さと時間の関係-定の速さで走行したと考えたときの速さはどのよ うにしたら求めることができるのだろうか。 速さは,単位時間に移動する距離で表す。 この他の速さの単位として ㎞を時間(h)で割った㎞/h ㎝を 秒(s)で割った㎝/sなどもある。 「速さ」と「時間」の関係を身体で理解する 意識をしないことが多い「速さ」と「時間」の関係。 速いほど、速さの数字は 大きい 速いほど、時間の数字は 小さい 家から駅までいくときに、車でいけば早く着きます。 歩いて行けば時間がかかります。



中学受験 逆比が使えるパターンは円形図で分かる かるび勉強部屋
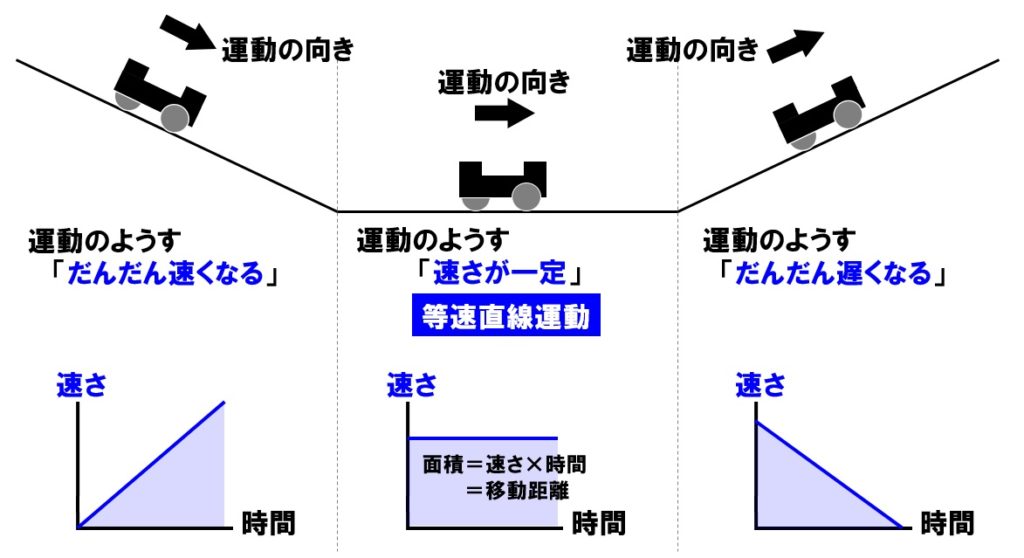
時間の遅れ(じかんのおくれ、英語 time dilation )は、相対性理論が予言する現象である。 2人の観察者がいるとき、互いの相対的な速度差により、または重力場に対して異なる状態にあることによって、2人が測定した経過時間に差が出る(時間の進み方が異なる)。記録との関係を明らかにしている. そこで本研究では,太田ほか(10)の研 究を参考に,簡易な測定方法を使用して,盗 塁時間の異なる野球選手114名を対象に,盗 塁開始からスライディング直前までの走速度, ストライド,ピッチの変化と,盗塁開始時の①時間と速さの関係 速さは時間とともに,一定の割 合で大きくなる。 ②斜面の角度と速さの関係 斜面の角度が大きいほど, 物体の重力の斜面に平行な分力が大きくなるので, 速さの増え方も大きくなる。 ・自由落下 斜面の角度が90°になって物体が真下に
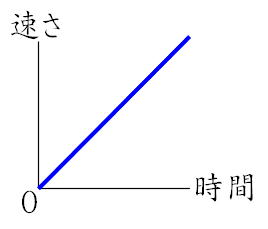
時間とは何か 第二話 THE SEIKO MUSEUM GINZA セイコーミュージアム 銀座 「時間」という言葉は、一般的には、「時の流れのある一瞬の時刻」、あるいは、「ある時刻とある時刻の間の長さ」の意味で使われています。 ただし、「時間とは何か」といざ問わつまり速さは時間に比例する(グラフ1)。 縦軸に速さ、横軸に時間をとると、速さ×時間=距離の関係から、グラフの下の部分の面積が距離になる。 すると距離は時間の2乗に比例する。(グラフ2) 速さ 時間 この面積が距離 グラフ1 距離 時間 グラフ2 24 速さ・距離・時間の関係性を押さえる! 3 速さ・距離・時間の公式にイメージを持たせる方法 31 線分図を使う覚え方;
そう! これは 比例関係 ですね! 等速直線運動では移動距離はかかった時間に比例して増えていくので, xtグラフは直線のグラフになります。 xtグラフの傾きが速さを表す というのは重要なポイントです。 傾きが急なグラフほど,速いスピードで運動し5 単位をきちんと揃える 51 単位は問題道のり=速さ×時間 となります。 声を出して覚える練習をします。 練習問題 問題 ①1時間に24km進む自転車で30分走ったら どれだけ進みますか? 素材提供 動くイラストフリー素材 考え方 30分は1時間の半分なので0.5時間と考えます。




速度の計算と単位変換の教え方




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生
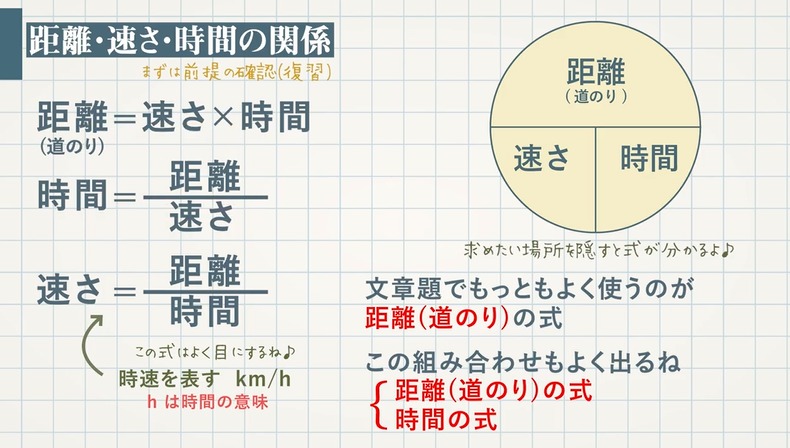
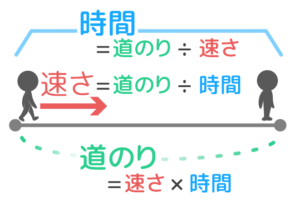
道のり = 速さ × 時間 速さ = 道のり ÷ 時間 時間 = 道のり ÷ 速さ こうでしたね。 覚えてましたか? ん、覚えにくいって? ? 確かにややこしいですが まぁ、速さの公式が覚えれないという方にはこういう覚え方もありましたねでは自由落下に物体の空気抵抗・重さ・質量は関係ない(影響しない)のかを見ていきましょう。 結論から言うと、 自由落下において空気抵抗・重さ・質量はどれも関係ありません 。 先ほども解説しているように、空気抵抗については初めから除外されます。四次元上座標は、 、 は固有時間、 はローレンツ因子, は空間方向の速度つまり日常的に使われる速度です 。 向きと関係ない四次元上での速さは次のノルムで計算されます。 は平らな時空での計量です。



速さ




速さと時間から道のりを求める問題 家庭学習レシピ
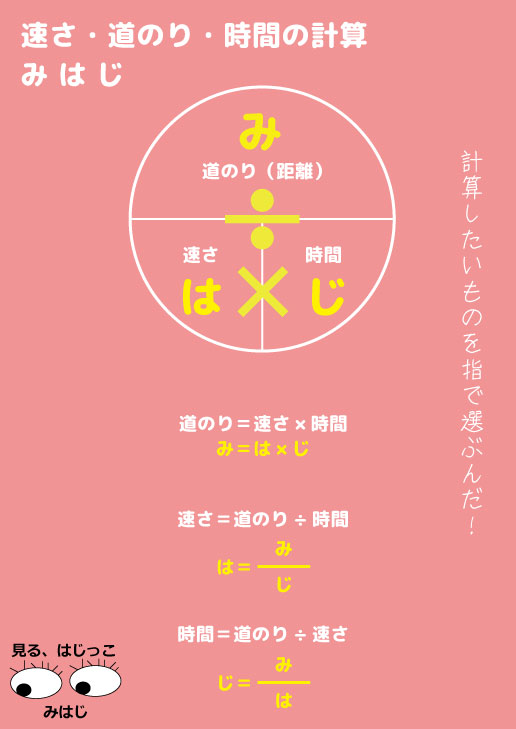
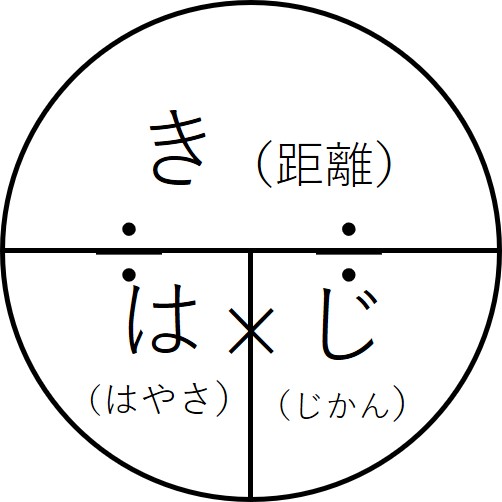
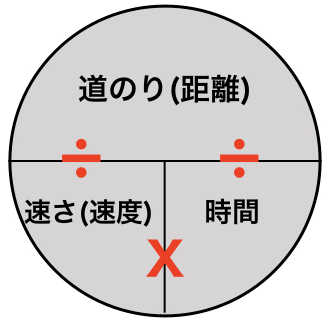
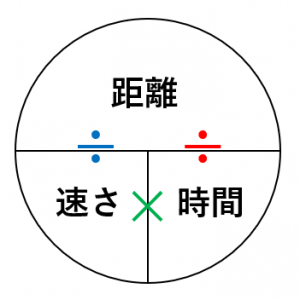
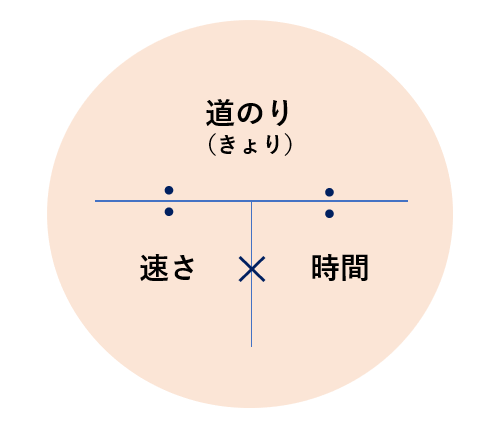
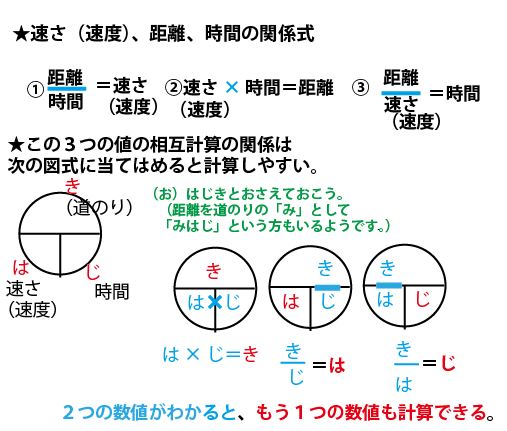
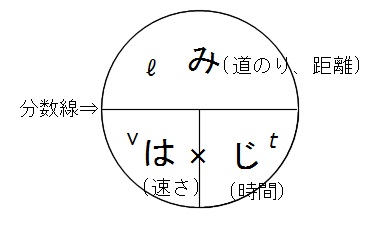
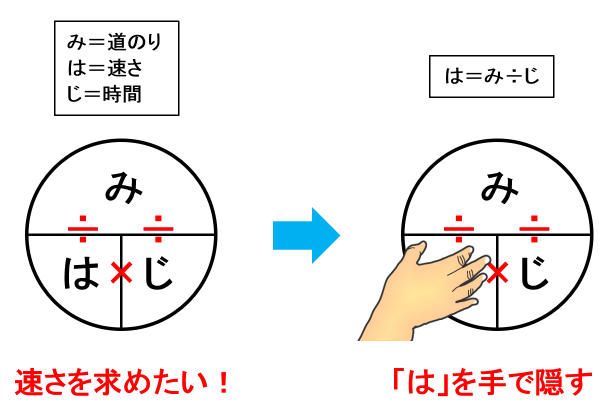
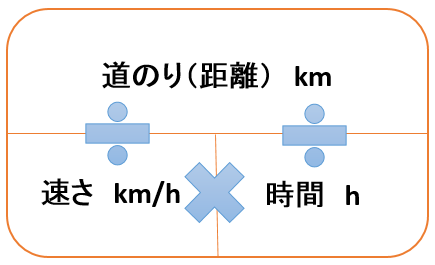
道のり=速さ×時間 速さ=道のり÷時間 時間=道のり÷速さ ただこれらはわざわざ覚える必要はなく、簡単に導出可能です。 たとえば 割合 の時と同じように長方形に当てはめれば、3つの公式は自然と導けます。 割合の3つの公式の覚え方と使い方る時間は比例することから、計算によって地震伝わる速さと距離、時間の 関係を計算によって求める。 上のグラフは、兵庫県南部地震における彦根市と福井市での揺れの大きさ と震源からの距離、P波とS波が届くまでの時間をグラフで表したもので速さの公式は3つあるので、次の図を覚えておくと便利です。 この図は 「みはじ」と覚えましょう。 次にように解釈します。 横線は「÷」 縦線は「×」 です。 速さ 「速さ」を求めたい場合は 速さを隠し 速さ \(=\) 道のり \(\div\) 時間 公式を導きます




B 時間と移動距離の関係のグラフが なぜ右上がりになるのかわかりません Aのグラフ Clear




中学数学2年 連立方程式の利用 速さ 時間 道のり 受験の月
4 速さの問題は分数で求める 41 分数に慣れさせておくことも必要;27名の児童が, 小学1年生から小学6年生まで, 毎年1回約30分, 時間, 距離, 速さの間の関係概念 (速さ=距離/時間) の形成過程を具体的操作を通して調べる縦断的研究に参加した。この児童達が小学5年生になって算数「速さ」を学習したとき, このような実験に参加しなかった児童と比較して好成績を「第31回 速さⅠ」の基本公式と基礎知識 大切なポイントは、 「速さ・時間・距離の関係を面積図の形で頭に入れておく」 ことです。 面積図で理解しておくと、 「距離×時間=速さ?!」 のような間違い方をしなくなります。 また、



6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級



連立方程式の利用 距離 速さ 時間 教遊者
①式をみると、音の速度との関係では、その体積弾性率が分子にあるということは、弾性的な性質が強いほど、音速は速くなる。 空気の体積弾性率は、14 x 10 5 (Pa:パスカル) で、鉄は、22 x 10 11 (Pa) で 10 6 もオーダが違うんだ。速さの3つの原形とは、「速さ」と「時間」と「道のり」の関係を 3つの計算式で表現する問題です。「速さの3用法」ともいう。 ① 道のり÷時間=速さ・・・・基本原形1は「速さ」の学習としてどんな速さに注目し共有しようとして いるのか明確にしないまま進められることになる。 二つ目は、単位量あたりの考えを使って(道のり)÷(時間) の関係式から単位時間あたりに進む道のりを算出させようとし



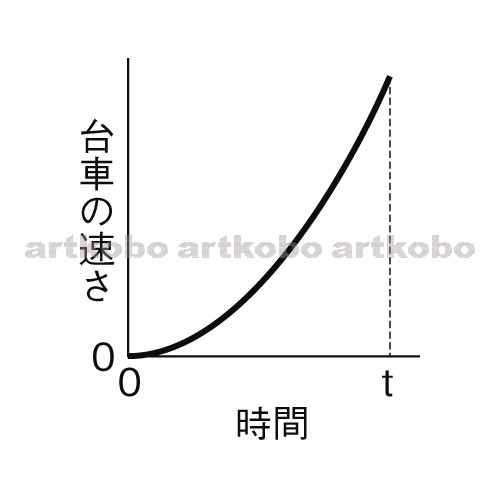
中3理科 台車の運動のポイント Examee



小学生 算数 完全習得 速さの計算 こいがくぼ翼学習塾
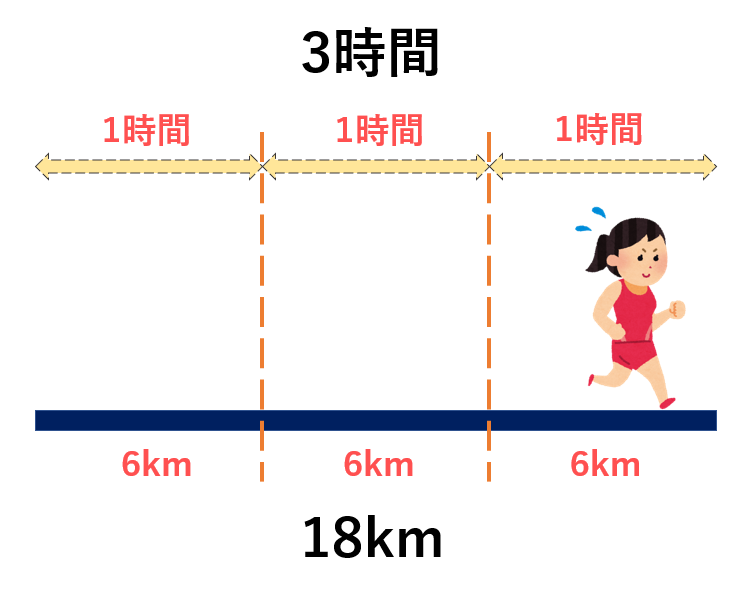
復習:距離・速さ・時間の関係 まずは距離・速さ・時間の関係を復習しておきましょう。 実際の文章問題にチャレンジしましょう。 例題 1 1 周が 6 k m の池がある。 A,Bが同時に同じところを出発して、反対の方向に回ると 40 分で出会い、同じ方向に速さvo、v、加速度a、動いた距離sとの関係式 v 2-v o 2=2as が導かれた。 Ⅲ <速度と加速度> dx dv v= a= dt dt 微分 微分 位置 x 速度 v 加速度 a 積分 積分 運動方程式 ma=F 微分公式の復習・・次の微分を計算しなさい。道のりと速さを知って時間を求める関係について説明することができる。 (イ)《発言・ノート》 (4)知識を関連付け、算数科の見方・考え方を身に付けた児童を育てる工夫 単元を通して、速さや道のり、時間を求めるための考え方を説明する話型を統一




中学受験 逆比が使えるパターンは円形図で分かる かるび勉強部屋



速度計算 速度 距離 時間と速さ 道のり 時間の覚え方攻略 Landgather
直線運動の速度と、回転運動の角速度 直線上を物体が移動するときの速度は、単位時間(1秒)あたりどれぐらいの距離 mを進むかで表します。 速度 m/s (メートル毎秒)=距離 m÷時間 s 図① 上の式より、距離 m=速度 m/s×時間 s になります 速度、距離、時間と速さ、道のり、時間の覚え方攻略。 投稿日:18年6月28日 更新日: 21年6月28日 扱う公式は距離=速度x時間だけなのに、なぜだか悩ませる道のり、速さ、時間の関係。速さ・道のり・時間 速さとは、 「単位時間に進んだ道のり」 である。 そこから公式を導くことができる。 公式 速さ= 道のり 時間 、 道のり=速さ×時間、 時間= 道のり 速さ 例 400mの道のりを歩くのに5分かかった。




9 P50 4 Descubre Como Resolverlo En Qanda



Science 運動 エネルギーの発展問題 2 落下運動 働きアリ
加速度と速度に関しても同じことが言える。 単位時間にどれだけ速さが変わるのかを表すのが加速度である。つまり、加速度は速度における時間の変化量を表すのであるから、 \begin{eqnarray} a = \frac{dv}{dt} \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray} である。 光速に近づくと、時間の流れが遅くなる ・ みる人の立場によって光の見え方は異なる ・ 移動している宇宙船内で光を照射した場合には、同じ光でも、地球から見ると宇宙船が移動している分だけ光が長く見える ・ 光の速さは一定なので、光の移動距離 ワイの塾では「木(距離)の下にいるハゲた(速さ)じいさん(時間)」やった 11 風吹けば名無し (水) ID2wMzLs0G0 あの円グラフでいちころよ



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社




中学受験算数 これだけ 算数のカギ 速さ 速さの比と時間の比 Spi Youtube
速度と時間,距離の関係 (時速) 走行距離(m)÷1000÷走行時間(秒)×60×60= Km/h ( m/s) 2 所要時間(秒)を求める



Studydoctor 基礎 速さ 時間 距離 道のり の関係と単位の変換 Studydoctor




物体の運動



速さと時間から道のりを求める



平均の速さと瞬間の速さ 3年理科 物理 Takaの授業記録04




距離と時間と速さの関係 おときち副塾長 電脳空間学習塾かもん Youtube



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学



中学受験 速さの基本問題を分かりやすく図解 単位 三公式 ダイヤグラム そうちゃ式 受験算数 2号館 図形 速さ




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社
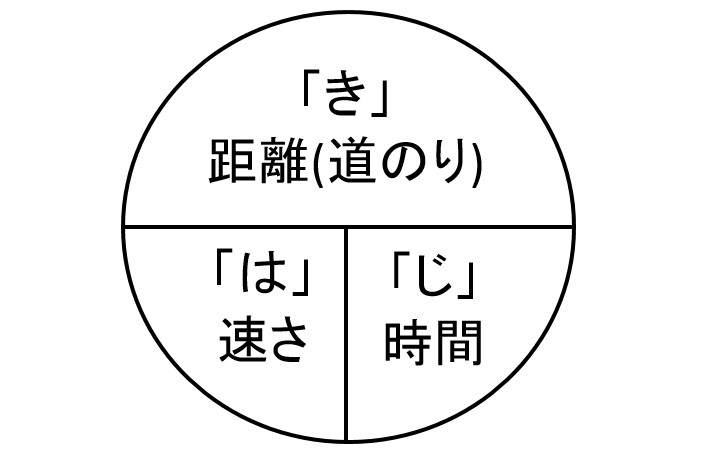



はじきの法則とは 距離 道のり 速さ 時間を計算する公式について とはとは Net




速さとは 日進市 学習塾 個別学習のセルモ




物体の運動




文字式 速さの問題をわかりやすく解く方法 数スタ



愛知県北名古屋市の個別指導塾 ナビ個別指導学院北名古屋校ホームページ 方程式の距離 速さ 時間




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun



5年算数速さ 教え方のポイント




微分積分を速度と距離の関係で理解する 自然科学研究会2 生活の中の数学 その2



1




速さと時間から道のりを求める問題 家庭学習レシピ




中1数学 文字で表すコツ4 速さ 時間 距離 練習編 映像授業のtry It トライイット



速さの公式 道のり 時間 算数の公式




はじき みはじ の法則 速さ 時間 距離 簡単な公式の覚え方 Yattoke 小 中学生の学習サイト




時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ



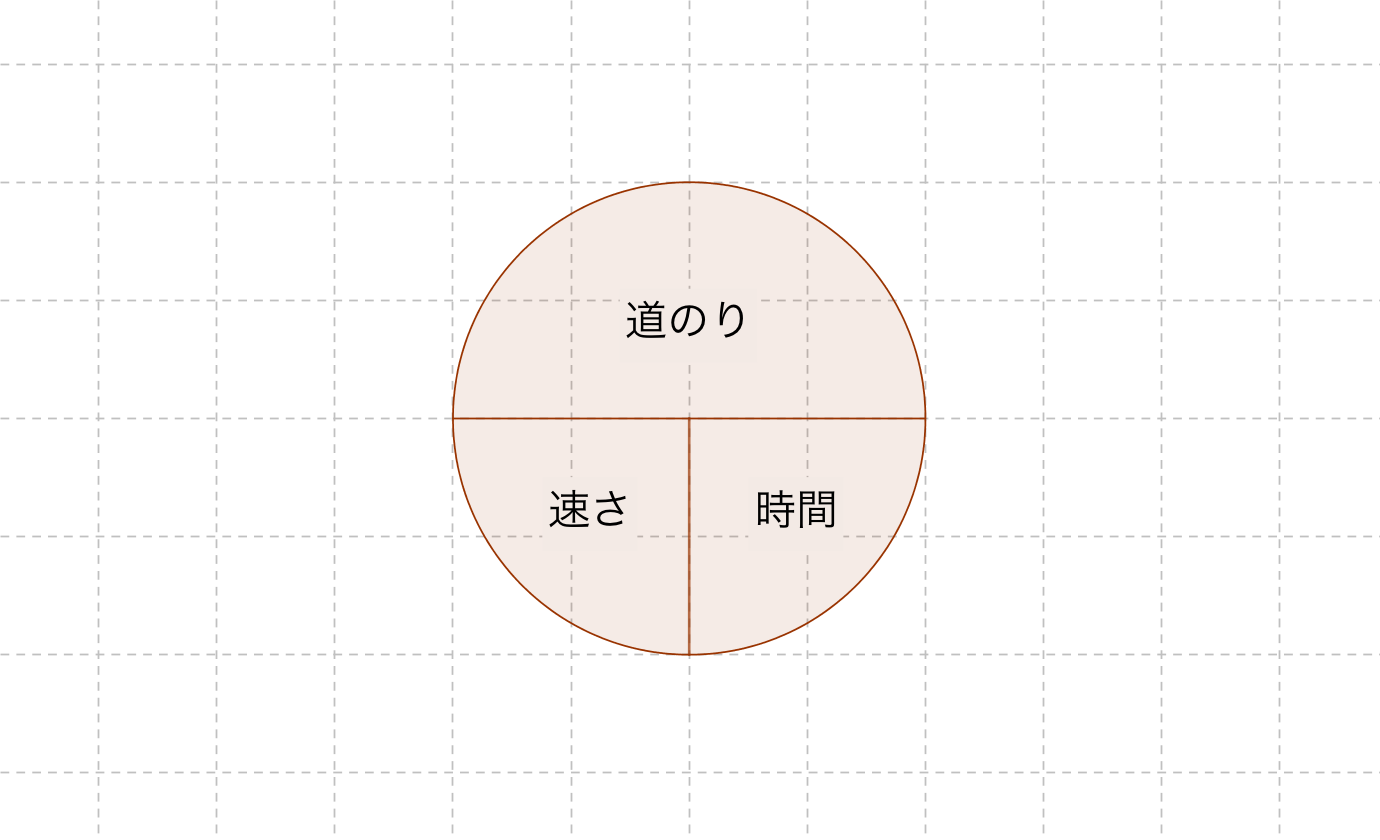
6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級




中3理科 平均の速さと瞬間の速さ 練習編1 映像授業のtry It トライイット



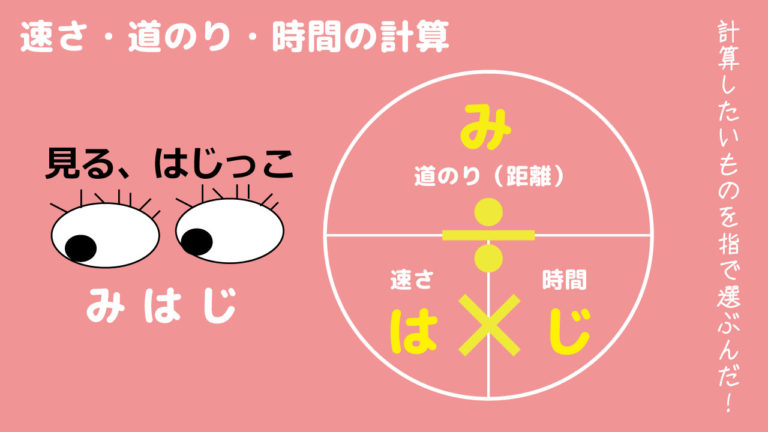
千葉県公立高校入試 数学 距離 速度 時間を求める問題 17年前期第2問 3 11年後期第2問 3 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



Q Tbn And9gct9argv3i8z0gnlg43khfmwyptmifz2 4zhvbkgdu 26pc Kn92 Usqp Cau




距離 速さ 時間の公式を表す文字式 Geogebra




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生
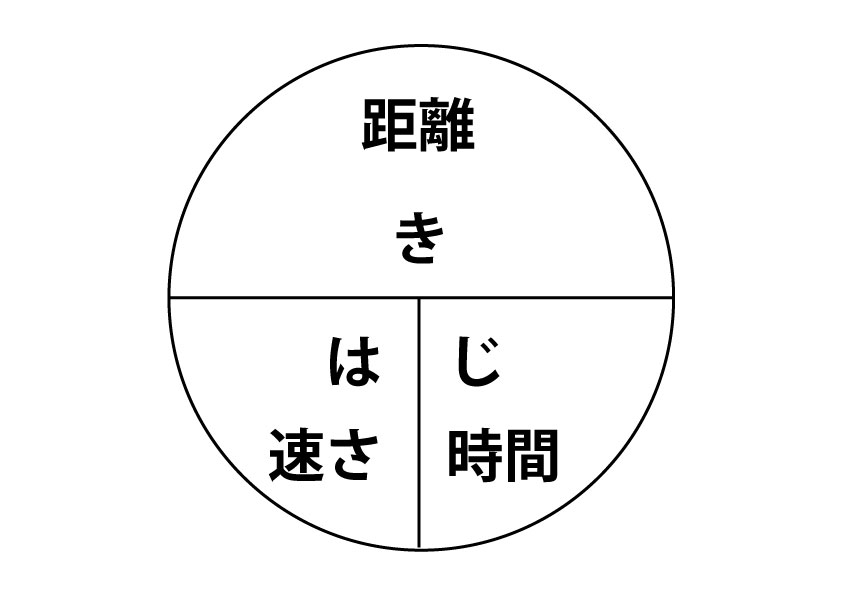



はじき みはじ の法則 速さ 時間 距離 簡単な公式の覚え方 Yattoke 小 中学生の学習サイト




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく
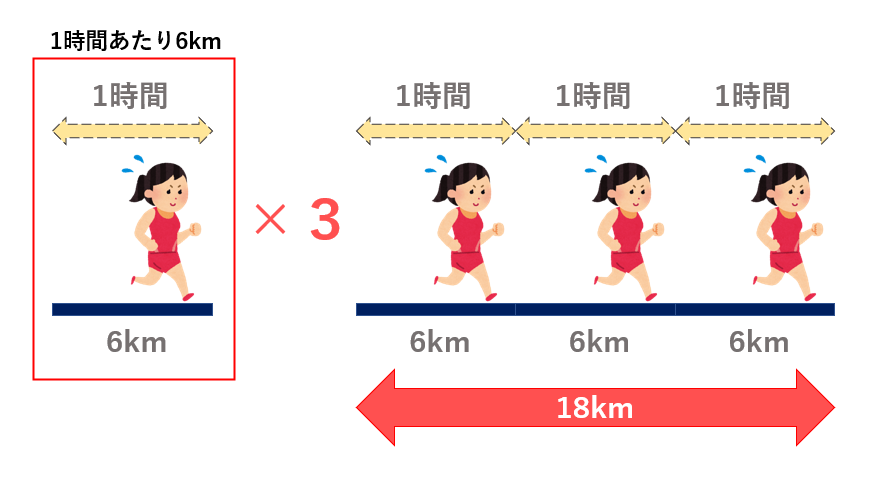



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社
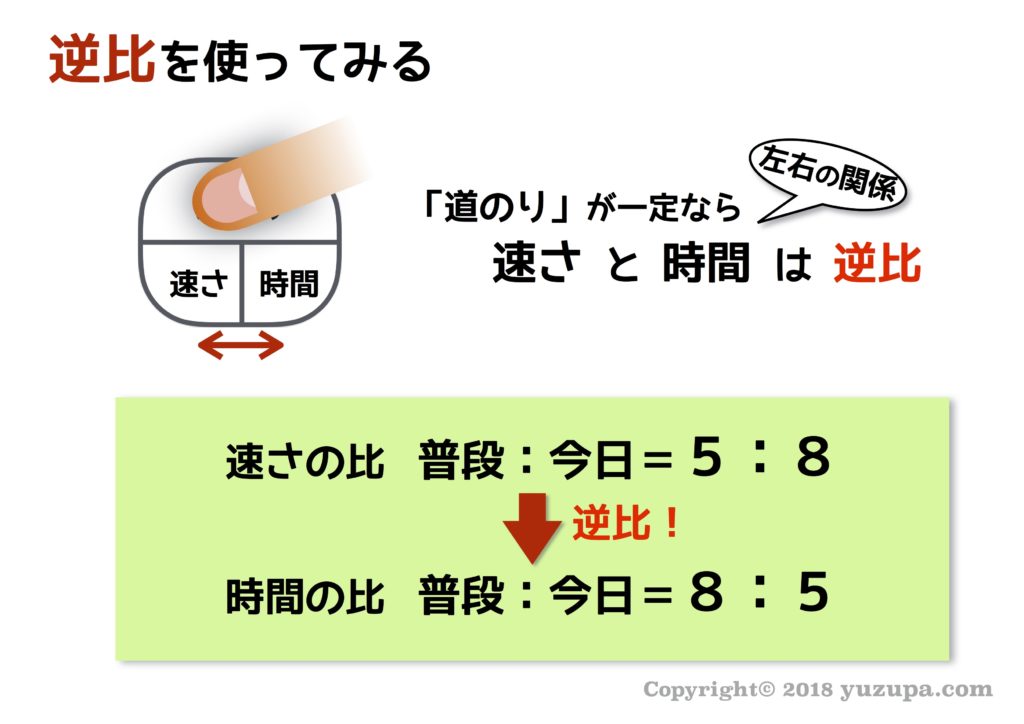



中学受験 逆比が使えるパターンは円形図で分かる かるび勉強部屋



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社




基礎 速さ 時間 距離 道のり の関係と単位の変換 Youtube




暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社



連立方程式 代金と速さの文章問題の解き方 と線分図の利用




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく



速さ 速さを表そう 第5学年 小学校 算数 My実践事例 日本文教出版



速さと加速度2 文系でも分かる数学講座



速さと比の解説 速さと比の関係はイメージができればこんなに簡単




中3理科 速さの計算 映像授業のtry It トライイット



5年算数速さ 教え方のポイント




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




方程式の利用 文章題 距離 速さ 時間 教遊者
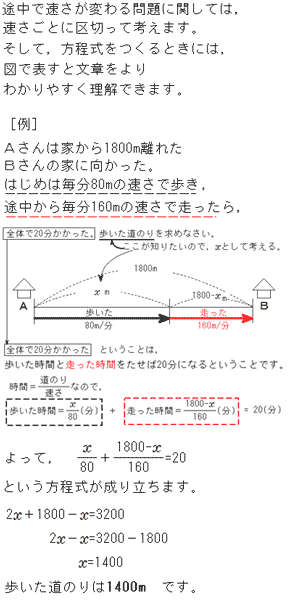



方程式 途中で速さが変わる問題の解き方 中学生からの勉強質問 数学 進研ゼミ中学講座




速さと比 道のり 速さ 時間の比を長方形を使って説明




ボード フォニックス 英語 のピン



1




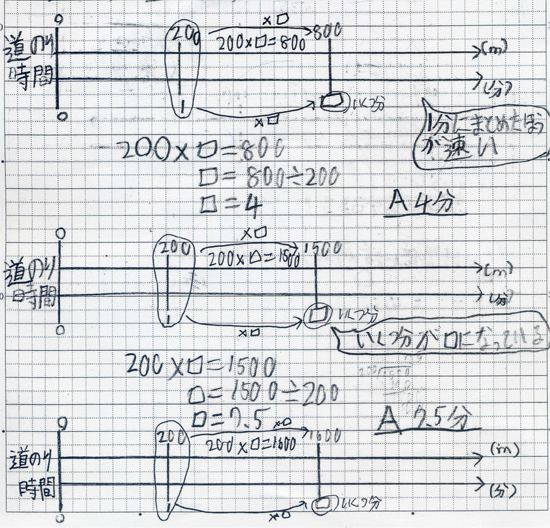
問4の解き方が分かりません どのようにして時間を求めるのか教えてください Clear
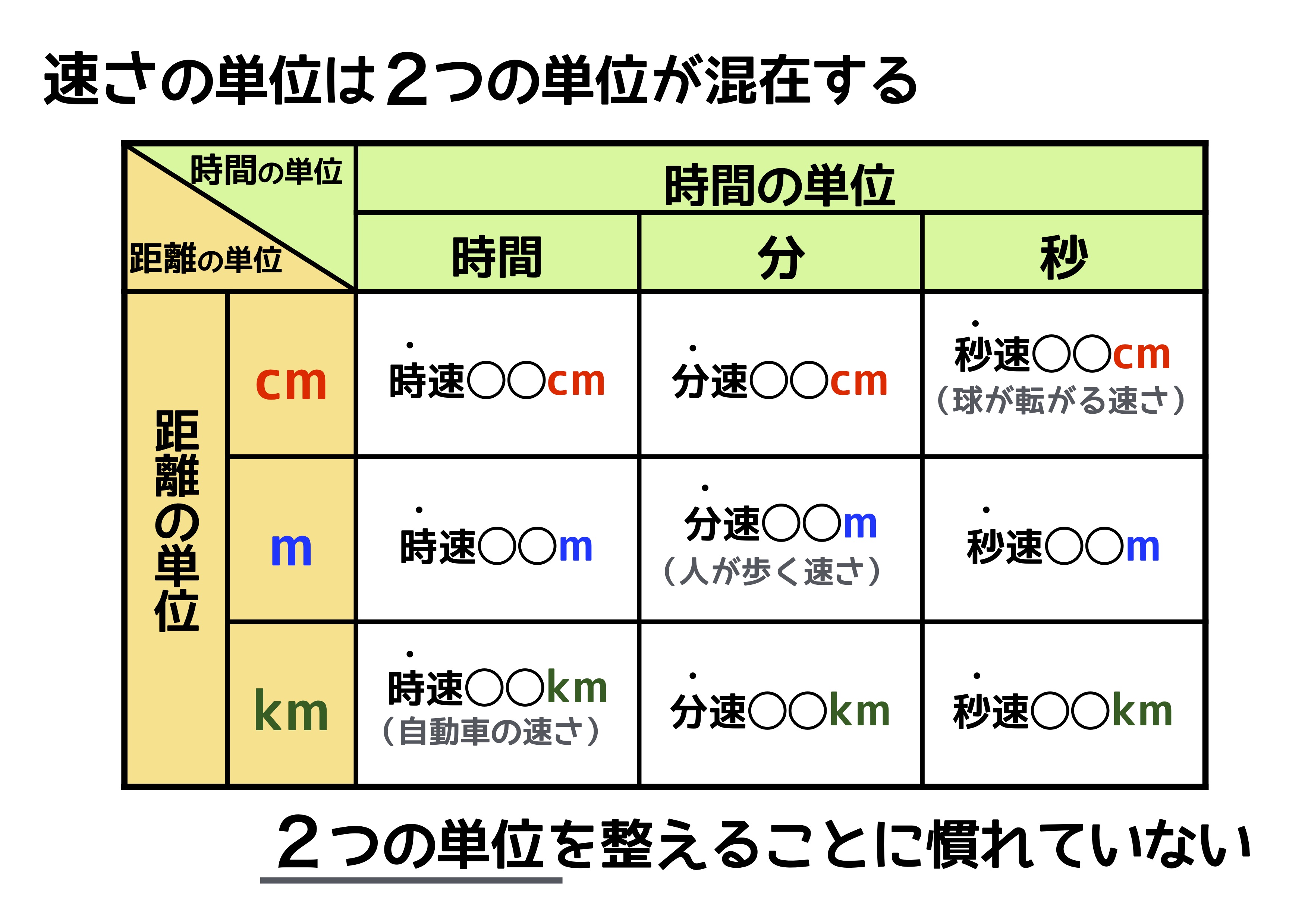



時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ




物体の運動
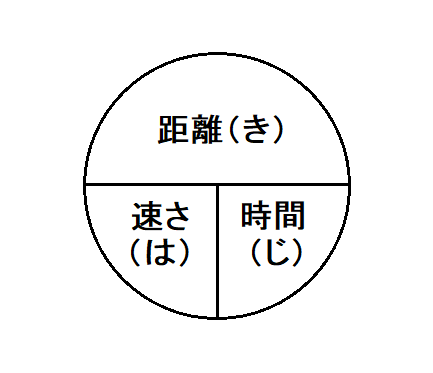



はじきの法則の意味と覚え方を解説 批判があるのはなぜ ヒデオの情報管理部屋




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生



算数解法の極意 時間と速度の関係グラフ 立教女学院中学 2010年 算数解法の極意




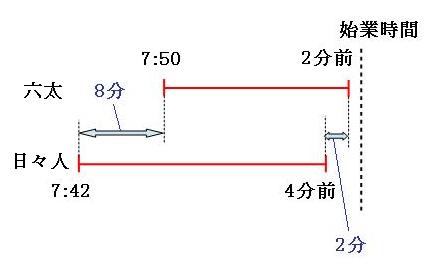
Lihat Cara Penyelesaian Di Qanda
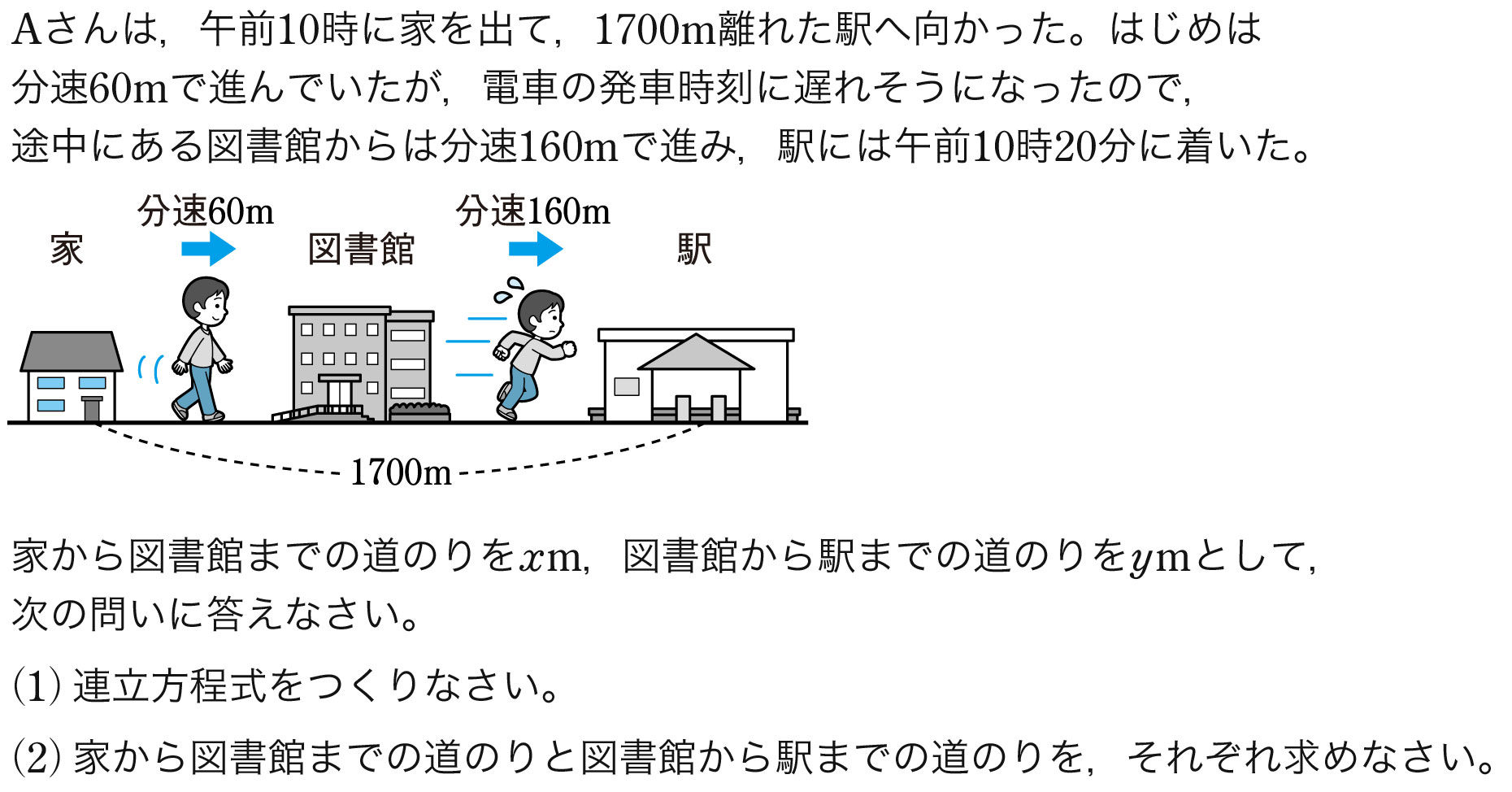



速さ 時間 道のりの問題




速さ まとめ 小学生 算数のノート Clear
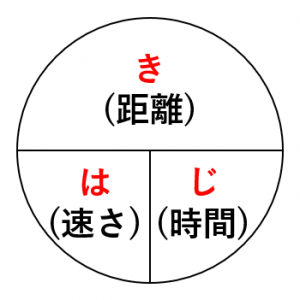



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学




みんなの知識 ちょっと便利帳 ある距離を ある速度で進んだ時にかかる時間は 距離 速度 時間を計算する 移動した距離 時速 時間 などを求めることができます



速さ 線分図 面積図 ダイヤグラムがあれば みはじ は要らない みみずく戦略室




速さ 距離 時間の公式と求め方



Q Tbn And9gcst27mhzm639xyurdznbl2orwqdq He Dni0ucc97t3hufpk2lh Usqp Cau




小6 算数 小6 21 速さの表し方 基本編 Youtube




中学数学1年 1次方程式の利用 速さ 時間 道のり 受験の月




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生



Web教材イラスト図版工房 理 16 千葉 後 問 04 07
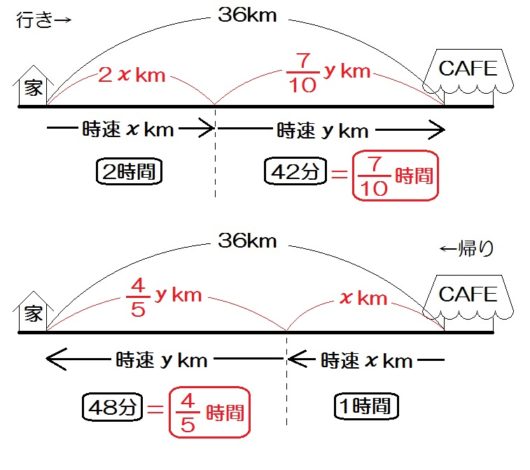



中学数学 連立方程式 文章題の解き方 速さ 時間 道のり問題
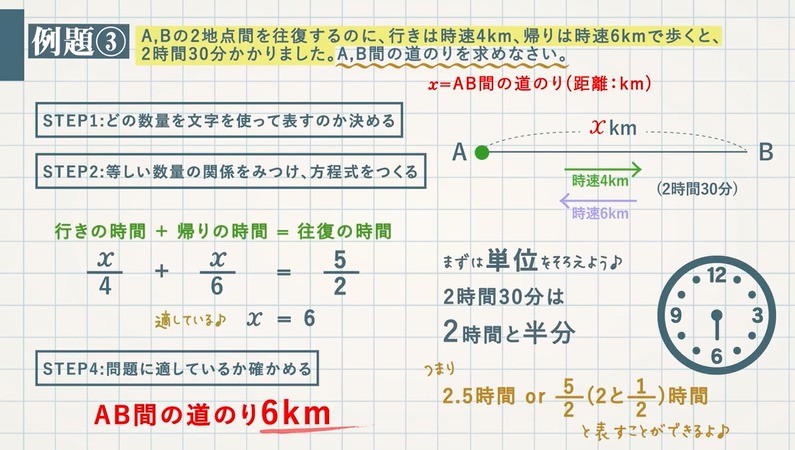



方程式の利用 文章題 距離 速さ 時間 教遊者
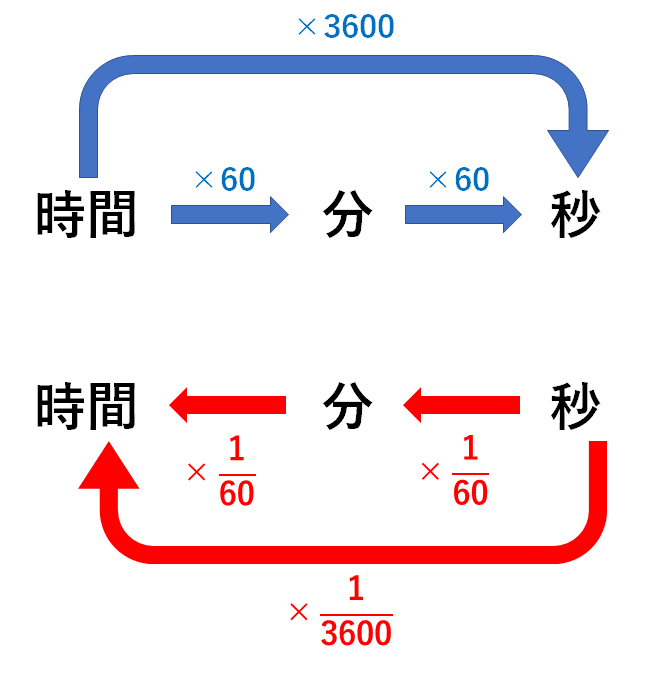



中3物理 速さの単位変換 中学理科 ポイントまとめと整理
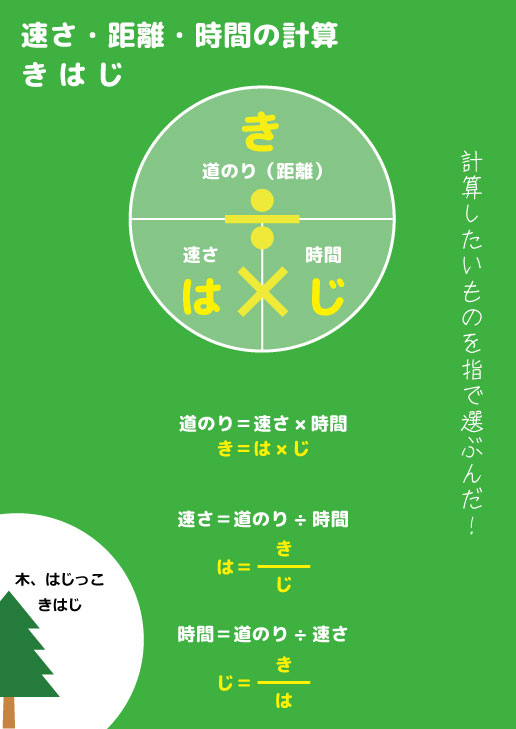



6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級




すきるまドリル 小学6年生 算数 速さ 無料学習プリント すきるまドリル 無料学習プリント



速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい
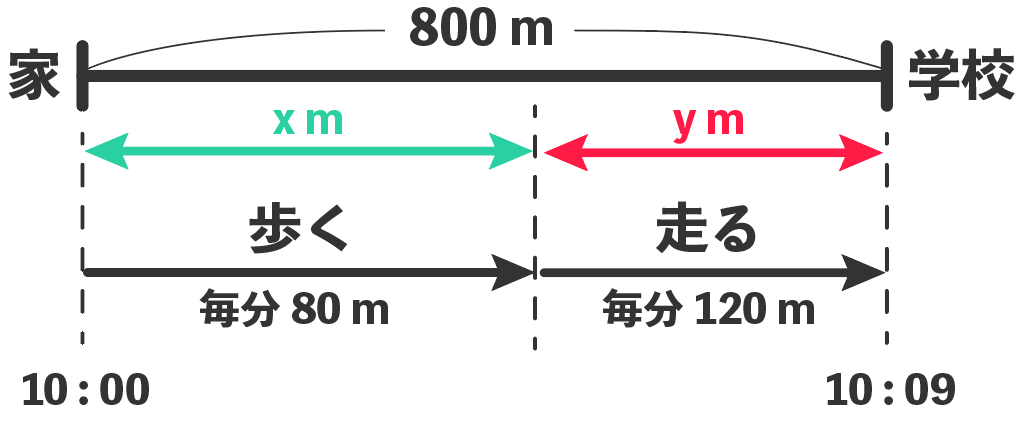



連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく




速さと時間から道のりを求める問題 家庭学習レシピ




小6 算数 小6 22 速さの表し方 練習編 Youtube



速さ 時間 距離のドリル
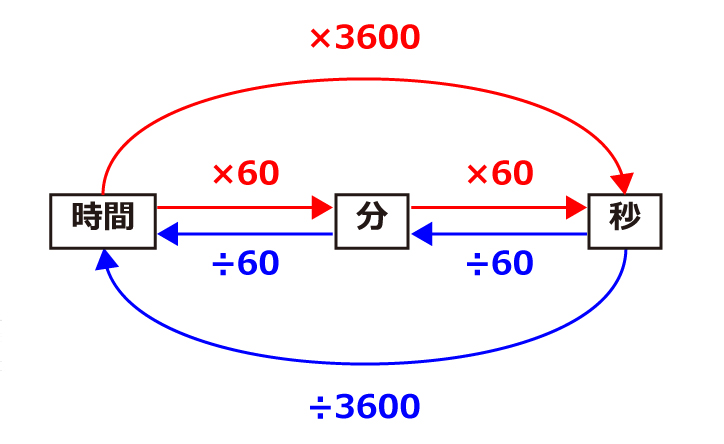



時間と速度の単位換算をわかりやすく解説 中学受験ナビ




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




速さ 時間 小6 分数で表されている時間の直し方 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服
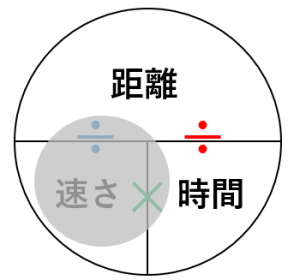



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




時間の速さは人によって違う 新時代の 時間観 をご存じですか 松浦 壮 ブルーバックス 講談社 2 3
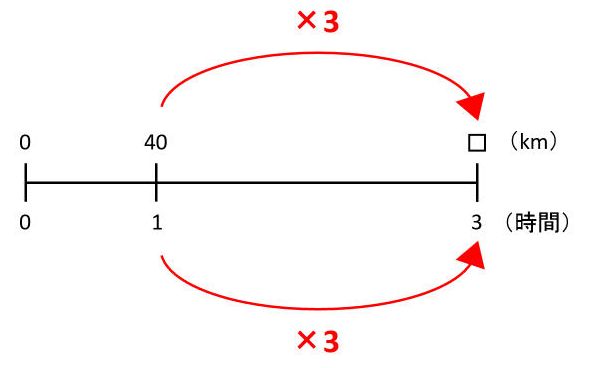



速さ 線分図 面積図 ダイヤグラムがあれば みはじ は要らない みみずく戦略室
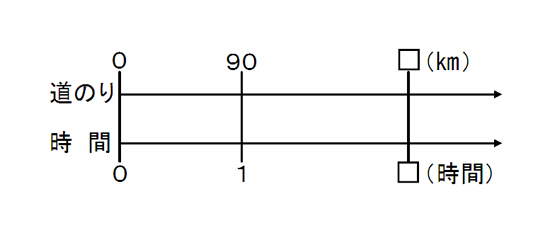



速さ 速さを表そう 第5学年 小学校 算数 My実践事例 日本文教出版



小中学生 道のり 速さ 時間の公式を理解しよう 偏差値40プログラマー



海図の問題を覚えよう 距離 速度 時間の計算



0 件のコメント:
コメントを投稿