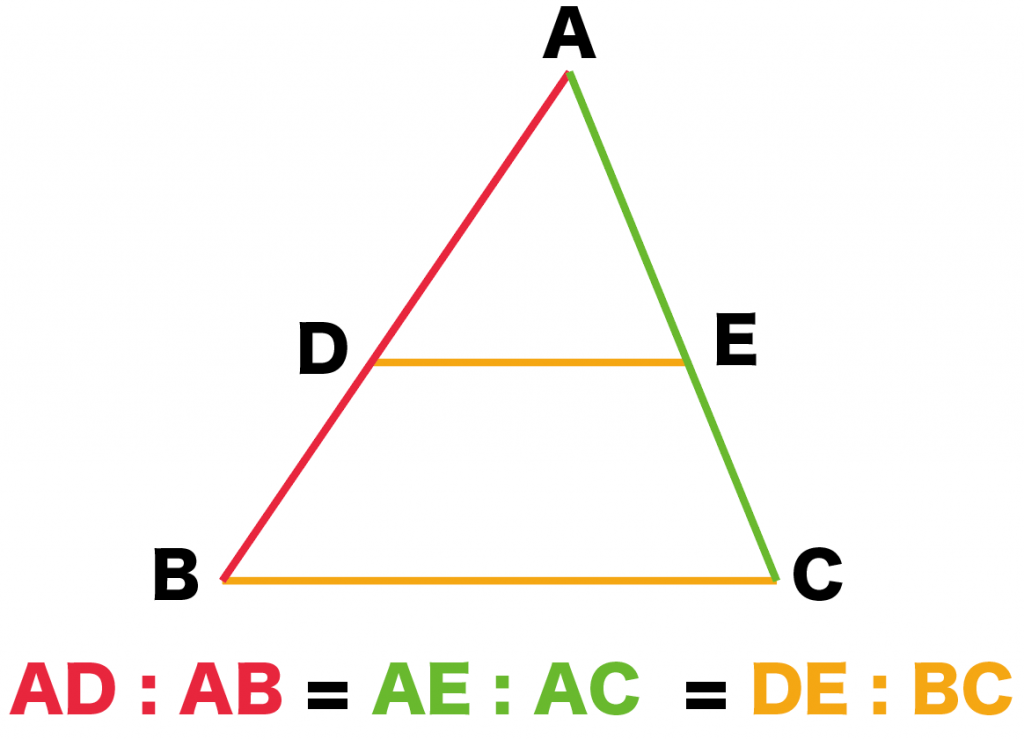
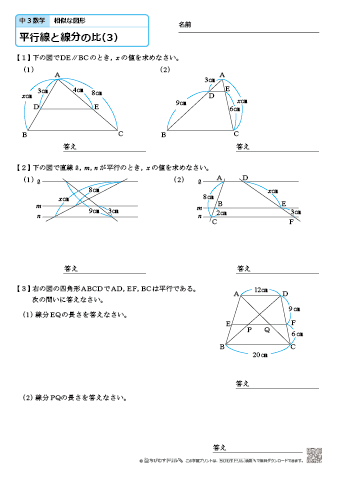
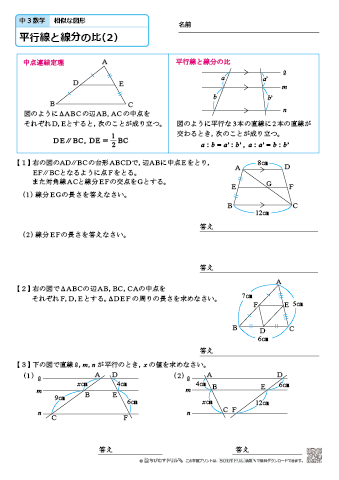
平行線と線分の比 下の図で、直線 \(l,m,n\) が平行ならば、線分の長さの比について以下のことが成りたつ。 \(abbc = deef\) これはなぜ成り立つのか。 下の図のように、\(df\) と平行な線分数学35章図形と相似「平行線と線分の比」<基本問題①・解答> 1 説明※平行線は,三角定規を利用してかく。 ①図のように線分AC上で点Aから 7番目の点と点Bを結ぶ。 ②点Aから5番目の点を通り,①で ひいた線分と平行な線分をひく。相似な図形 平行線と線分の比21 無料で使える中学学習プリント http//chugakumanabihirobanet/ 2 解答 ①ℓ ②ℓ m m 1 6

平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
線分の比と平行線
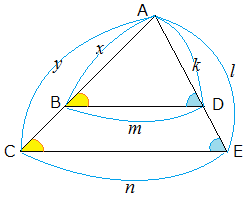
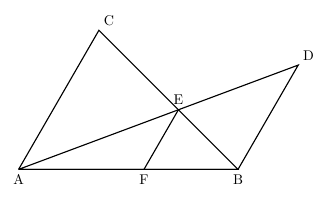
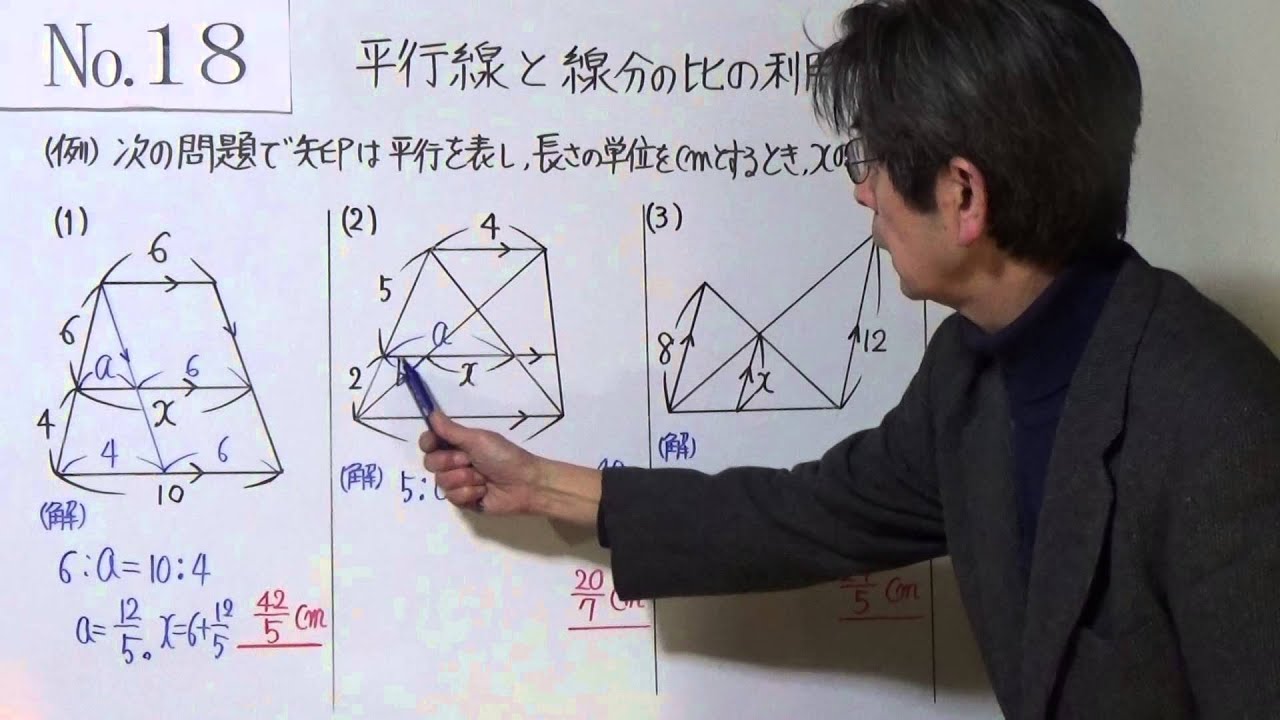
線分の比と平行線-(平行線に着目) よく使われる相似 acに対角線をひきefとの交点をgとする。 2 3 5 5 g ef//bcより∠aeg=∠abc(同位角), ∠a共通となるので aeg∽ abc(2組の角がそれぞれ等しい。) 同様に cgf∽ cad aegと abcで aeeb=23なので aeab=25 (注) よって相似比が25 egbc=25 eg=25 eg=8平行線と線分の比 上の図3のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. bd//ce のとき まず




中3数学 平行線と比4 線分比 平行 練習編 映像授業のtry It トライイット
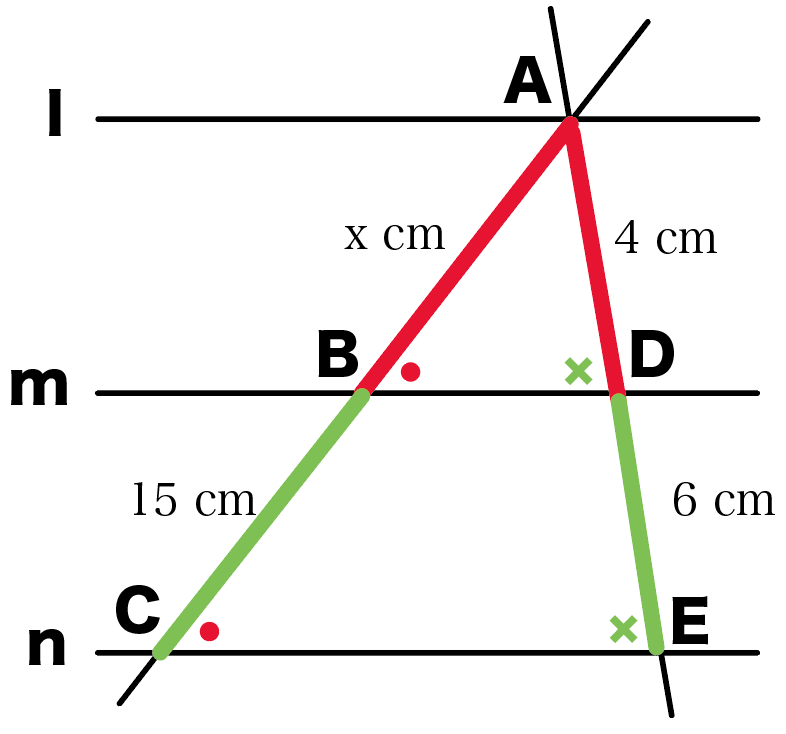
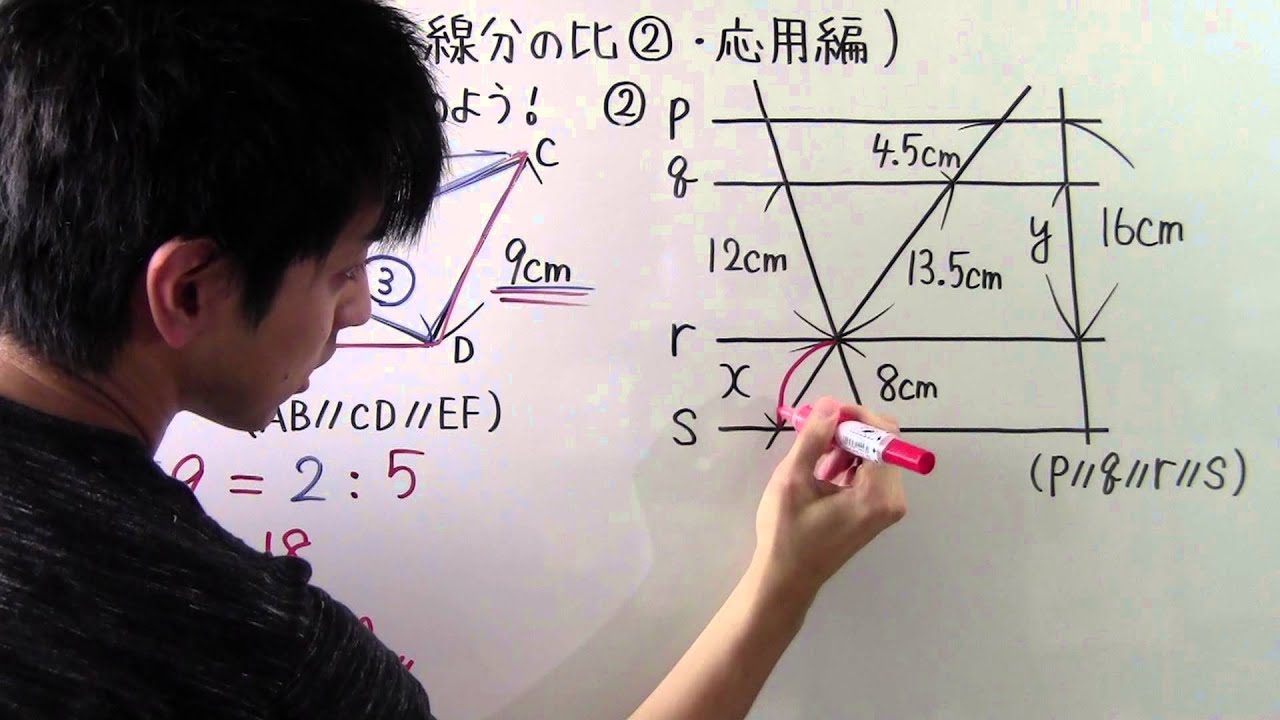
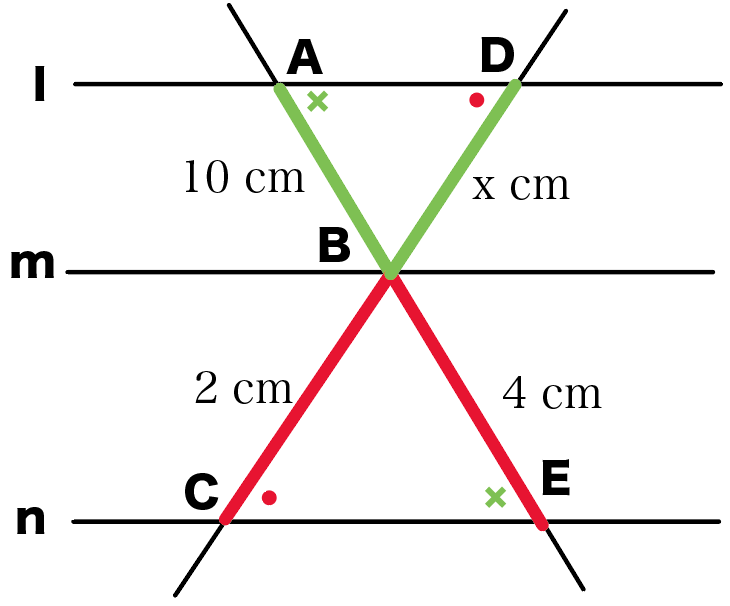
平行線と線分の比の問題の解き方3ステップ さっそく、 平行線と線分の比の問題 を解いてみようか。 l//m//nのとき、xの値を求めなさい この手の問題は3ステップでとけちゃうよ。 対応する線分を見極める 比例式をつくる 比例式をとく Step1 対応する・ 線分の比と平行線の性質を利用して、問題を解決することができる。 段階 学習活動 数学的活動を通した指導のポイント ( は数学的活動をともなう学習活動)3 平行線と線分の比 「平行線に直線が交わるとき、その交点の間の比は等しくなる」ことを次のように 証明した。直線l,m,nが平行であるとき、かっこに当てはまる語をうめよう。 点aを通り、直線a′に平行な直線を引き、それと直線m,nの交点をd,eとした。
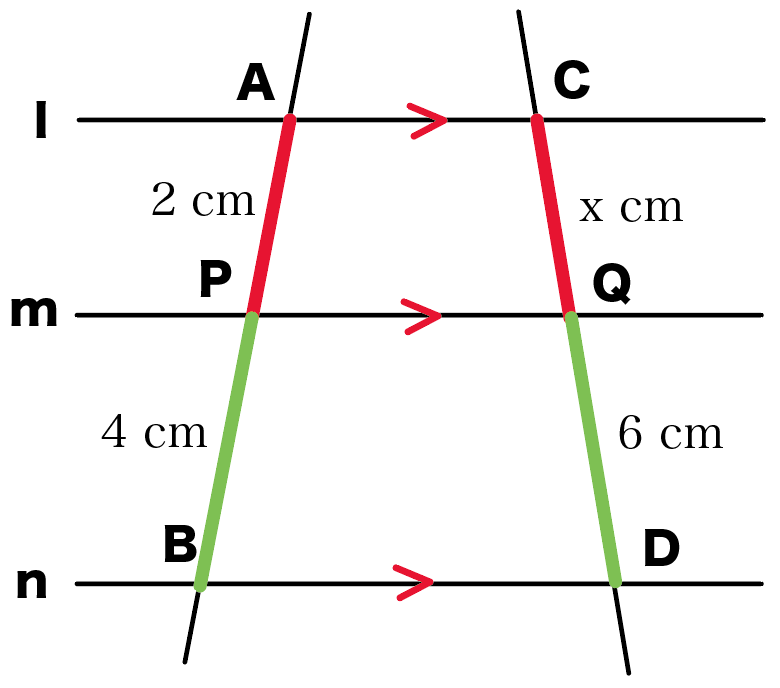
平行線と線分の比 右の図で,AB == PQ == CD である。 a b x A B C D P Q AB = a;平行線の比 実際平行線の比というものを見る前に内分点と外分点について知っておこう。 とある線分ABがあり、その内部に点PがありAP:PB=m:nのとき、 点PはABをm:nに内分しているという。相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru相似な図形 平行線と線分の比11 無料で使える中学学習プリント http//chugakumanabihirobanet/ 2 解答 ①PQ//BCならば2/5時 ・ 平行線と線分の比に関する性質を理解する。 ・ 平行線と線分の比の性質を利用して、辺の長さを求めることができる。 前時のまとめを基に、平行線と線分の比の性質について確認する。 本時の学習内容「平行線と線分の比の関係について




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
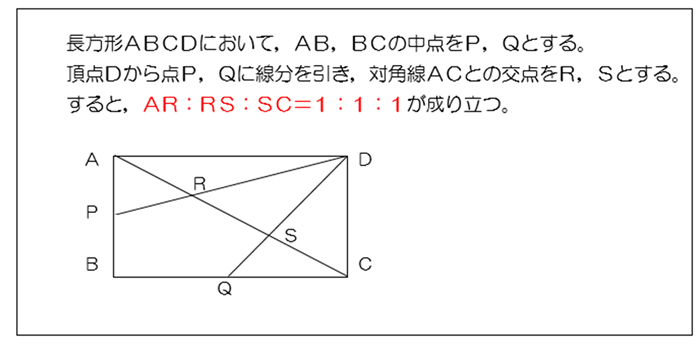



授業実践記録 数学 新しい 定理 とその活用 啓林館
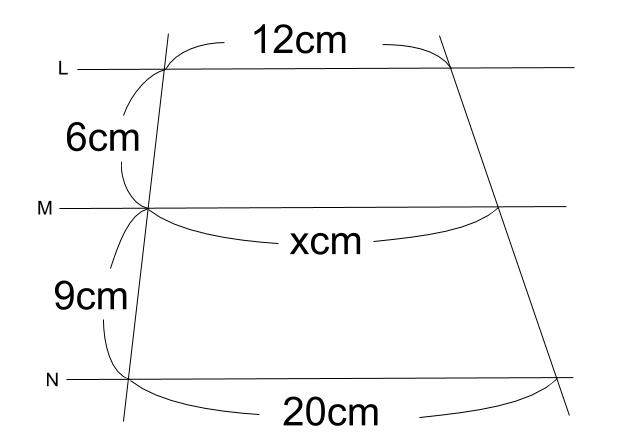
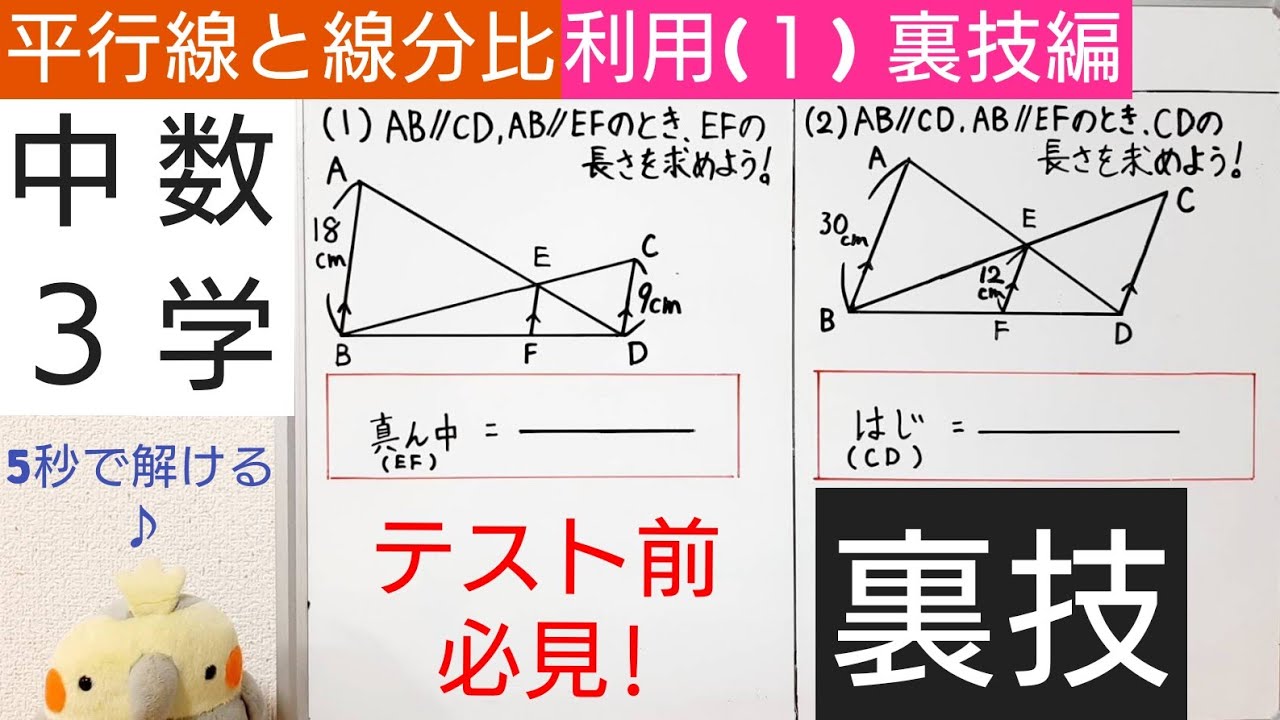
P132 線分の比と平行線 大晦日の夜に学校の近くの山の山頂で明日の初日の出を見ようという約束をしたとしま しょう。いよいよその元日の朝起きてみると日の出はまだですがうっすらと空が明るくな っていて、「いかん、日の出に間に合うかなぁ?平行線と線分の比 直線が平行線と交わるときにできる線分の比について考えてみよう。 下の図を考えよう。 平行な 3 つの 直線a、b、c に 直線l、m が交わっ ている。 AB:BC=2:3 だけれど、 DE:EF の比はどうなっているかな? 点A から 点F を結ぶ線分平行な $3$ 本の線のうち、左と右の長さがわかっているときは、$\rm ABE$ と $\rm DCE$ からスタート STEP $\textcolor{blue}{1}$ : $\textcolor{blue}{\rm ABE∽ DCE}$ $\rm ABDC=9cm12cm=\textcolor{blue}{34}$ (相似比) POINT:対応する線分の長さの比は、すべて等しい



至急 平行線と線分の比の逆の証明を教えてください Ad Db Yahoo 知恵袋




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
平行線と線分の比で下の写真の三角形の比が 22+3=25 とあったのですがこの式はいったいどういう理屈で出てきたかわかりません 何故22という 比が出てきて更に3を足すのですか、何線分 ec と対角線 bd との交点を f とし,点 f を通って辺 bc に平行な直線と辺 ab との交点を g とします。 このとき,線分 EG の長さを求めなさい。 (埼玉県17年入試問題) 単元 平行線と比, 「 授業ノート🌸 見にくかったらごめんなさい🌐 ♡・コメント・フォロー 待ってます🗽🗽🗽」, 学年 中学3年生, キーワード 平行線と相似,平行線と線分の比,中点連結定理,相似比



平行線による比の移動




平行線と線分の比 無料で使える中学学習プリント
平行線と線分比 新しい教材 正則関数の最大値を調べてみよう。 平方根の利用 コピー用紙相似な図形 平行線と線分の比22 無料で使える中学学習プリント http//chugakumanabihirobanet/ 2 解答 ①ℓ ②ℓ m m 1 6平行線と線分の比 右図2のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. bd//ce のとき まず




線分比の移動の公式を教えてください よろしくお願いします Clear



Http Www Fdtext Com Dat Suub3 5zukei 2senbunhi Pdf
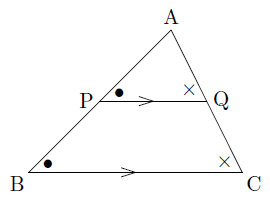
PQ = x とするとき, x = ab a b が成り立つ. £ ¢ なぜ、この補助線を書いたかというと、 この補助線があると、平行と線分比の関係をうまく使えるからなんじゃ 具体的に見ていくかのぉ まず、ax xd を考えてみるかのぉ 図で考えると、ax xd というのは、以下の感じじゃ平行線と線分の比 まとめ 以上、7パターンの問題について解説してきました。 おそらくこれらのパターンをしっかりと理解できていれば ほとんどの問題には対応できるのではないかと思います。 比の取り方は、練習で身につけていくのが一番です。



第5章7 平行線と線分の比 三角形と平行線 フロントエンドなブログ
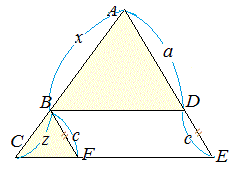



平行線と線分の比
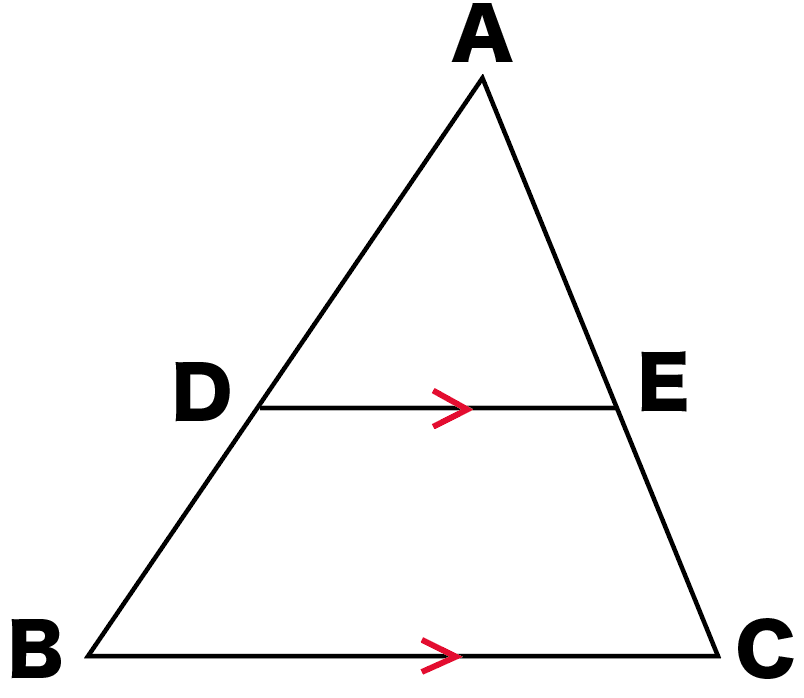
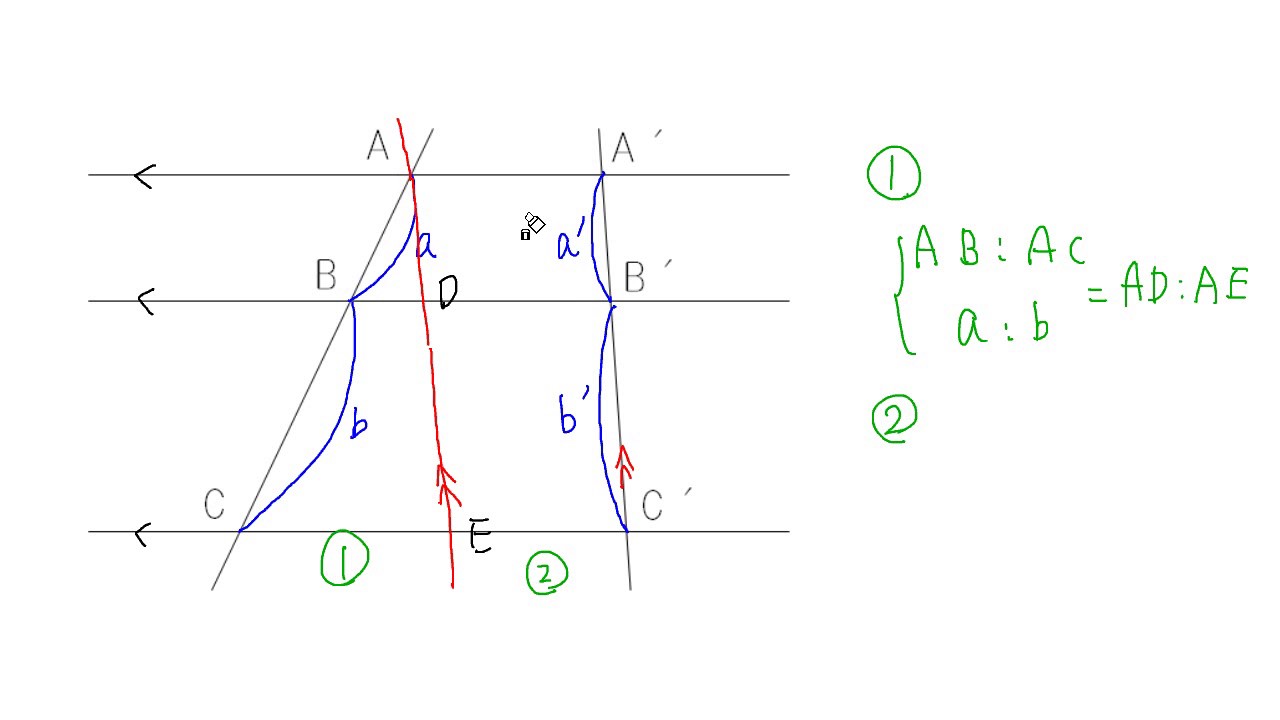
4 平行線と線分の比 平行な直線がある2つの三角形の線分の比について1 abc でpq¥bc のとき、 apq は abc と相似になる。 <証明> apq と abc において pq¥bc より、 平行線の同位角は等しいから ∠apq =∠abc ① ∠aqp =∠acb ② (∠a が共通も使えるけどね)100 こんにちは。今回は神奈川県の入試問題より, 平行線と線分の比に関する問題です。それではどうぞ。 図において, 四角形abcdは平行四辺形である。また, 点eは線分bc上の点であり, 三角形abeは正三角形である。さらに, 線分abの中点をfとし, 線分aeと線分cfとの交点をgとする。平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\) が平行
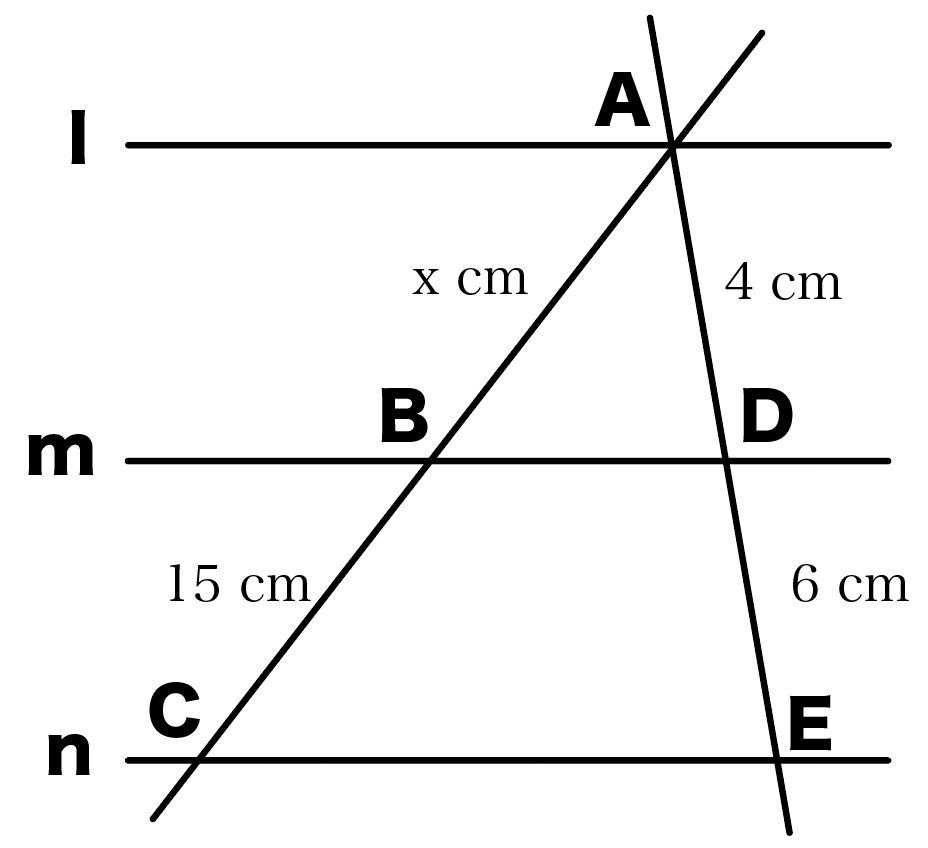



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
== 相似図形,平行線と比 == ※ 問題数は4題ではありません.合計13題あります. 問題1 _____ 第1問 / 全3問中平行線による比の移動 まずはどこに平行線を引くか考えますよね? まずはADDBが2:1であることに注目して緑線の補助線を引きます。 すると、、、 緑線とAEの交点からAまでとEまでの比は2:1になります。 そして線分CDに注目するために2:1を4:2にする 平行線の線分比の問題の解法 19/1/18 相似 ホームページのリニューアルに伴い一部のページは新しいサイトにリダイレクトされます。



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
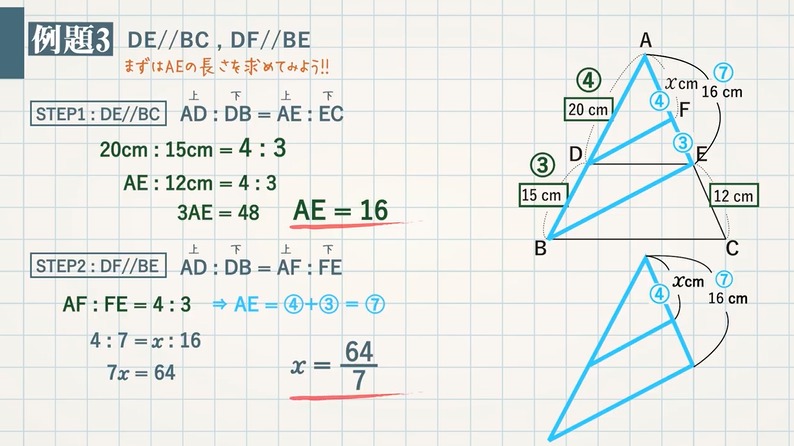



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
FdData 中間期末:中学数学3 年:平行線 三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内



平行線と線分の比



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平行線と線分の比 Ict教材eboard イーボード
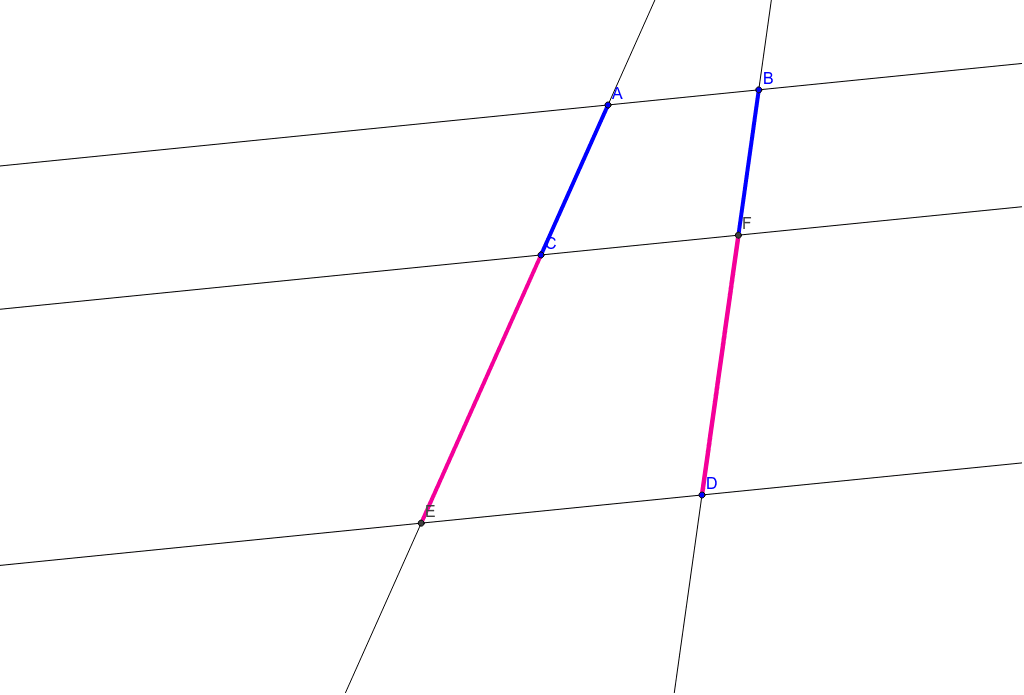



平行線と線分の比 Geogebra
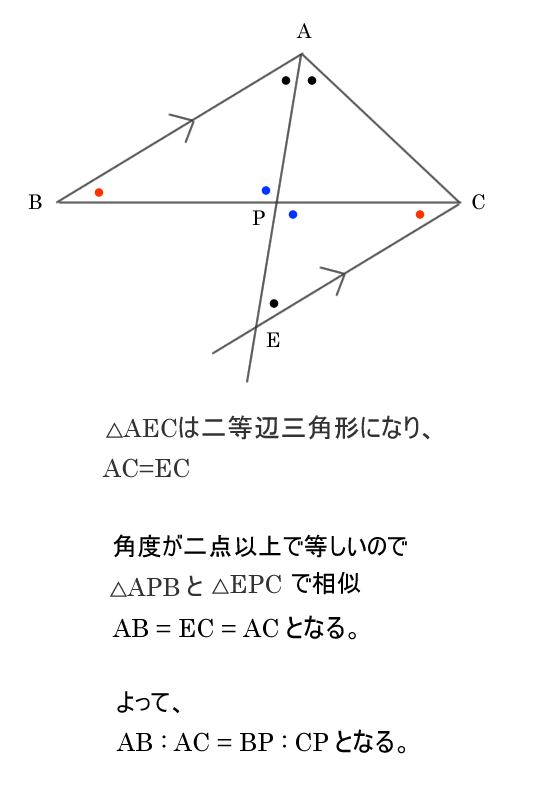



角の二等分線定理 証明 優技録



平行線と線分の比の定理の逆は成り立たない反例を教えて下さい 図を描 Yahoo 知恵袋
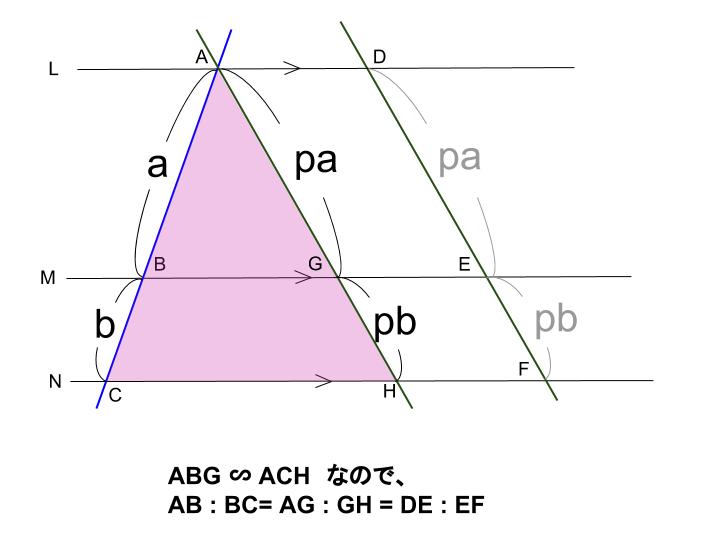



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor
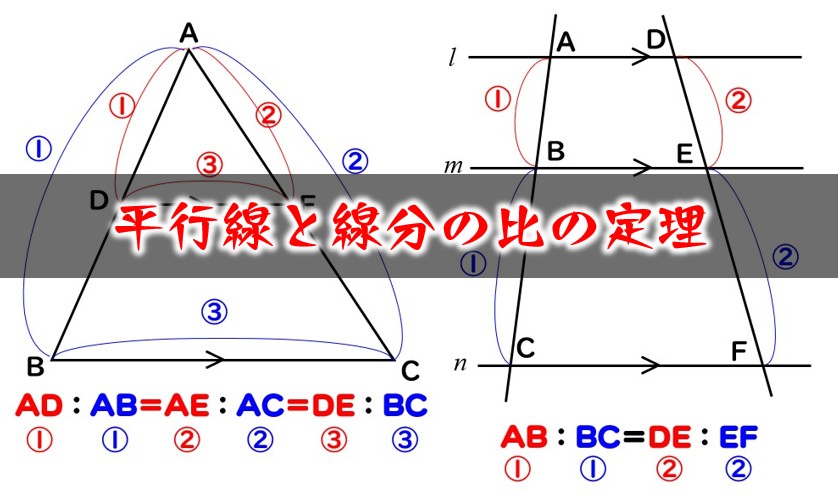



平行線と線分の比の定理 の問題の解き方 数学fun




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット




中3数学 相似の平行線と線分の比のポイントと定期テスト対策問題




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張




線分の比と平行線について 中3 家庭教師とっしゅ先生の授業 小学生 中学生
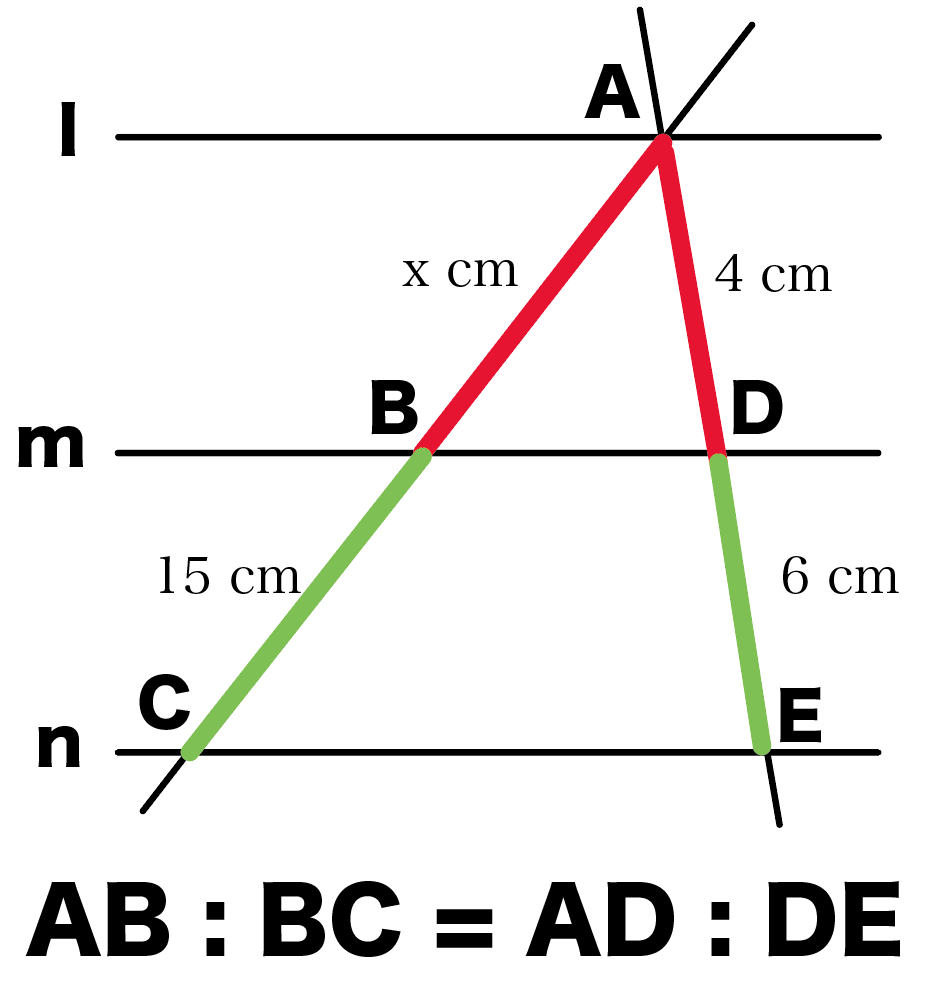



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
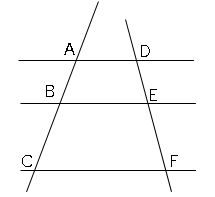



平行線と線分の比と中点連結定理 数学の要点まとめ 練習問題一覧




勉強しよう数学 10月 17



平行線と線分の比についてです この図形に平行線と線分の比があるのですが Yahoo 知恵袋



高校入試 英語 数学 図形と相似 平行線と線分の比




平行線と線分の比の問題 平行な3つの直線が2つの直線と交わっています 数学 教えて Goo
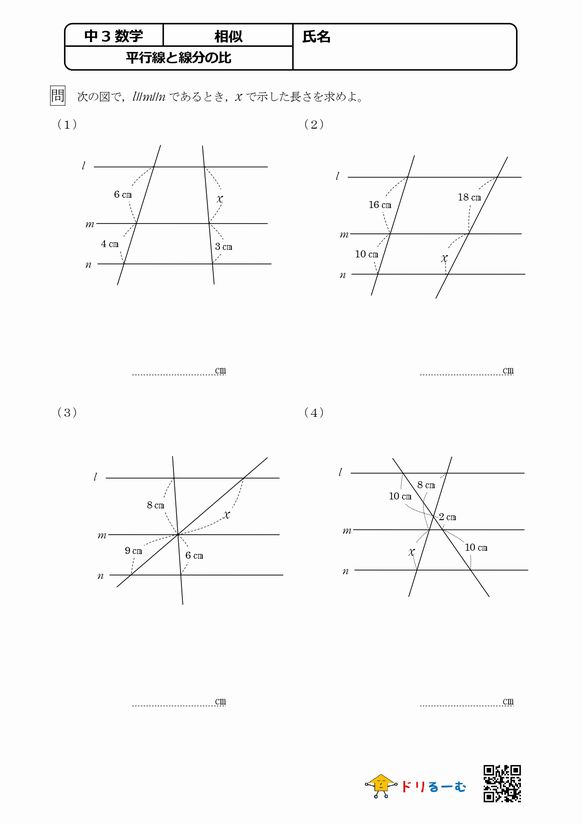



相似 平行線と線分の比 ドリるーむ
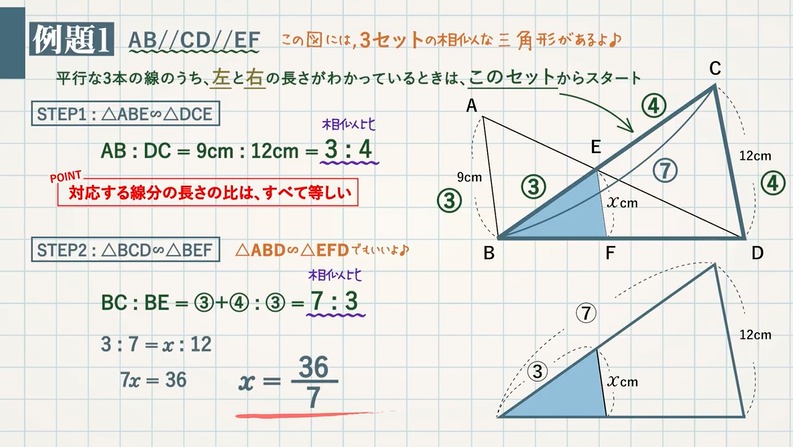



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
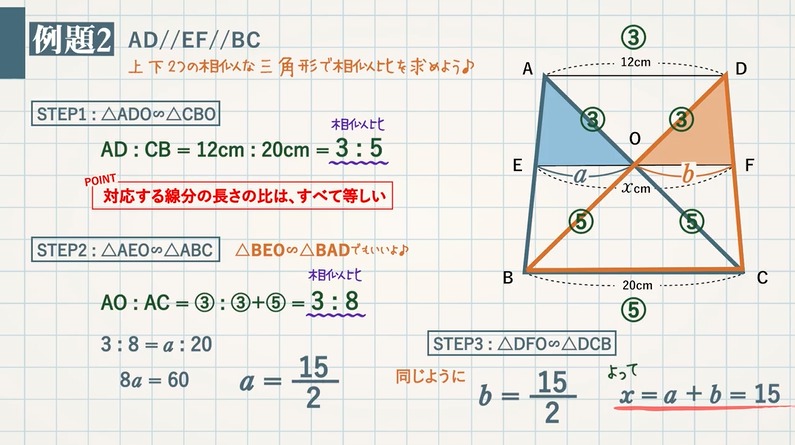



平行線と線分の比 辺の長さを求める応用問題4選 教遊者




平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題




中3数学 相似な図形 平行線と線分の比 同じ向きの三角形の場合 Youtube



Q Tbn And9gcs8yek Ytk4aevkupzlfiomyr1swah7y0fxr8n2 Yhcmpzyumt Usqp Cau




数学 平行と線分比をシッカリわかると メネラウスの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




角の2等分と線分の比 高校数学の無料オンライン学習サイトko Su



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



平行線と線分の比



1



中学3年生の数学 平行線と線分の比の利用 下の図で Yahoo 知恵袋



平行線と線分の比 まなびの学園



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Studydoctor平行線と台形 中3数学 Studydoctor



平行線と線分の比 中学3年 数学クラブ




中2 相似 平行線と線分の比 中学生 数学のノート Clear




中3 20 1 線分比と面積比 1 Youtube




中2 相似 平行線と線分の比 中学生 数学のノート Clear
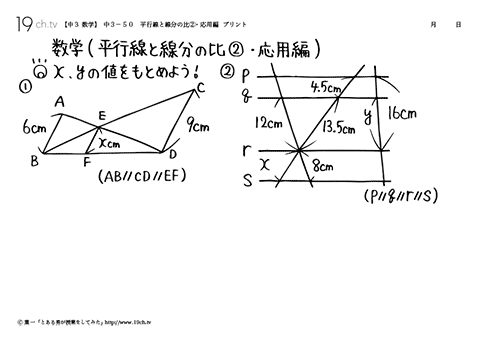



中学3年の数学 動画 平行線と線分の比 応用編の問題 19ch



相似 平行 三角形と線分の比 勉強ナビゲーター
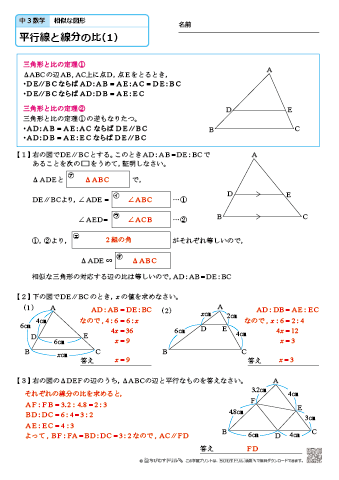



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
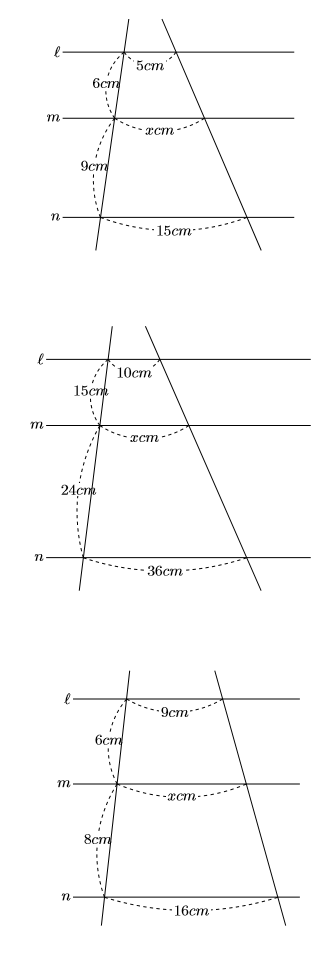



中学数学 中3平行線と線分の比 数樂管理人のブログ



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



平行線の線分比の問題の解法 夢を叶える塾




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア




平行線にはさまれた線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




数学 中3 49 平行線と線分の比 基本編 Youtube



中3数学 15 平行線と線分の比の利用 1 裏技 Youtube




数学 中3 51 平行線と線分の比 中点連結定理編 Youtube



数学 中3 50 平行線と線分の比 応用編 Youtube



平行線と線分の比 中学3年 数学クラブ




中3数学 平行線と比3 平行 線分比 映像授業のtry It トライイット



中学校3年生の数学の授業




中学3年数学練習問題 図形と相似 平行線と線分の比の問題




平行線と線分の比 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中3数学 平行線と比4 線分比 平行 練習編 映像授業のtry It トライイット



中3 18 5 平行線と線分の比の応用 Youtube




中3数学 相似と線分比1 平行四辺形 Youtube
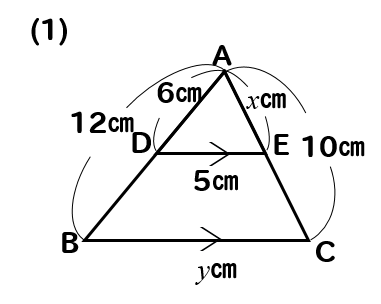



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




中3数学 図形と相似23 平行線と線分の比 比の合成 連比 すべて無料 星組の中学数学講座



平行線と線分の比の問題です Xの値を求めるのですが やり方が分かり Yahoo 知恵袋




数学 平行 と 線分比 の関係についてまとめました 知っておくと応用がきくよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




平行線と線分の比 の問題を参考に 問題へのアプローチを 現役医師による難関高校受験塾 Core コア



平行線による比の移動
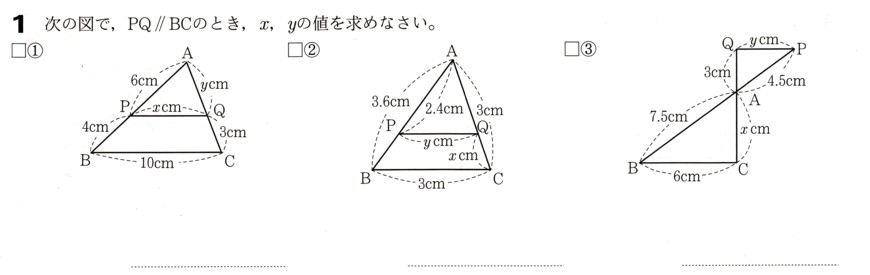



中学3年数学 図形と相似 平行線と線分の比 練習問題1 あんのん塾




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
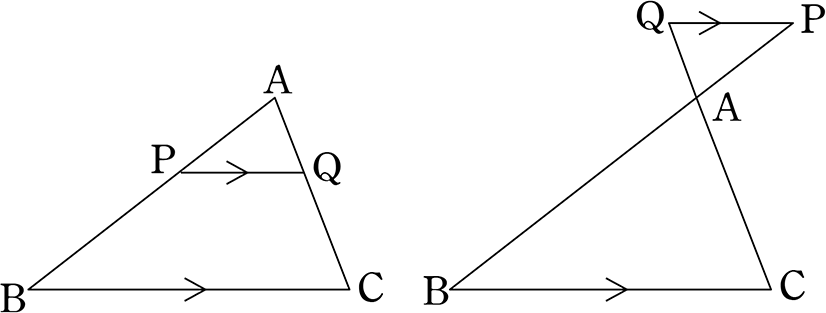



中学数学 図形の相似



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



中3数学 平行線と線分比の利用のポイントと練習問題



平行線と線分の比 中学3年 数学クラブ



1




中3数学 相似な図形 平行線と線分の比 同じ向きの三角形の場合 Youtube



第5章10 平行線と線分の比 三角形と平行線 中学生
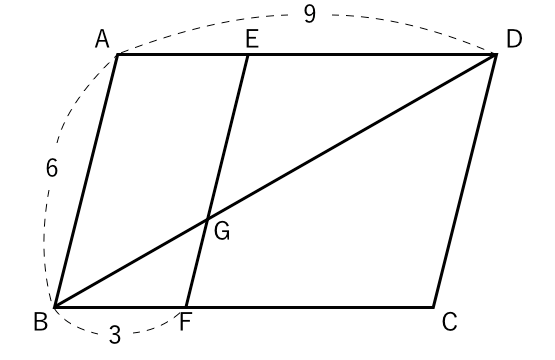



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
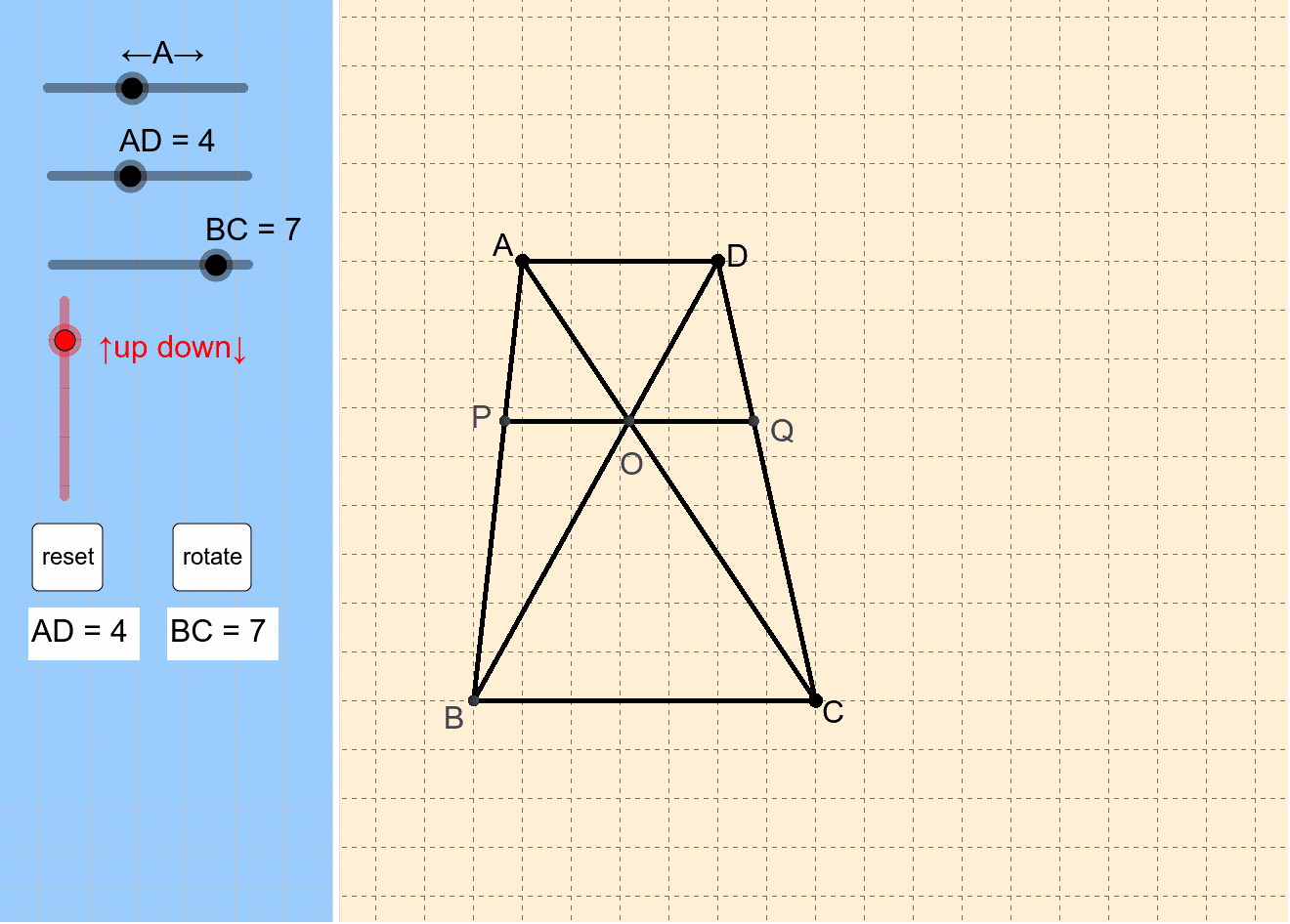



相似 平行線と線分の比 Geogebra



1
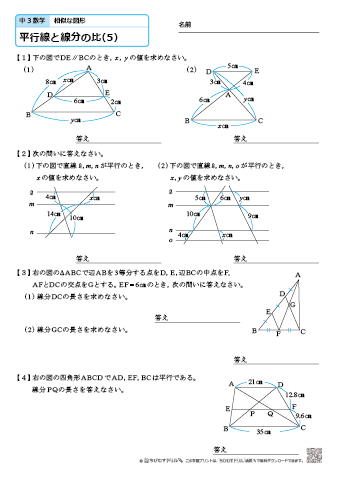



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
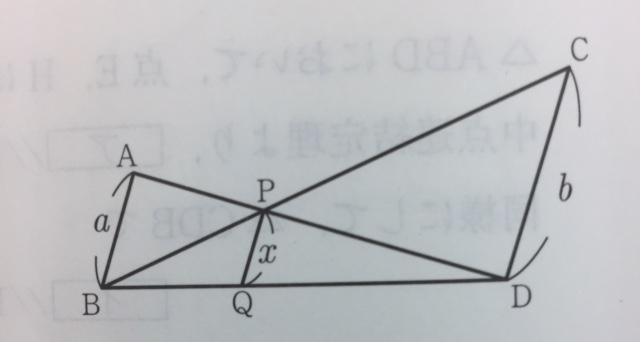



相似 平行線と線分の比 石川県金沢市の個別塾 学習塾 ナビ個別指導学院 泉が丘校ブログ




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平行線と比 Mp4 On Vimeo
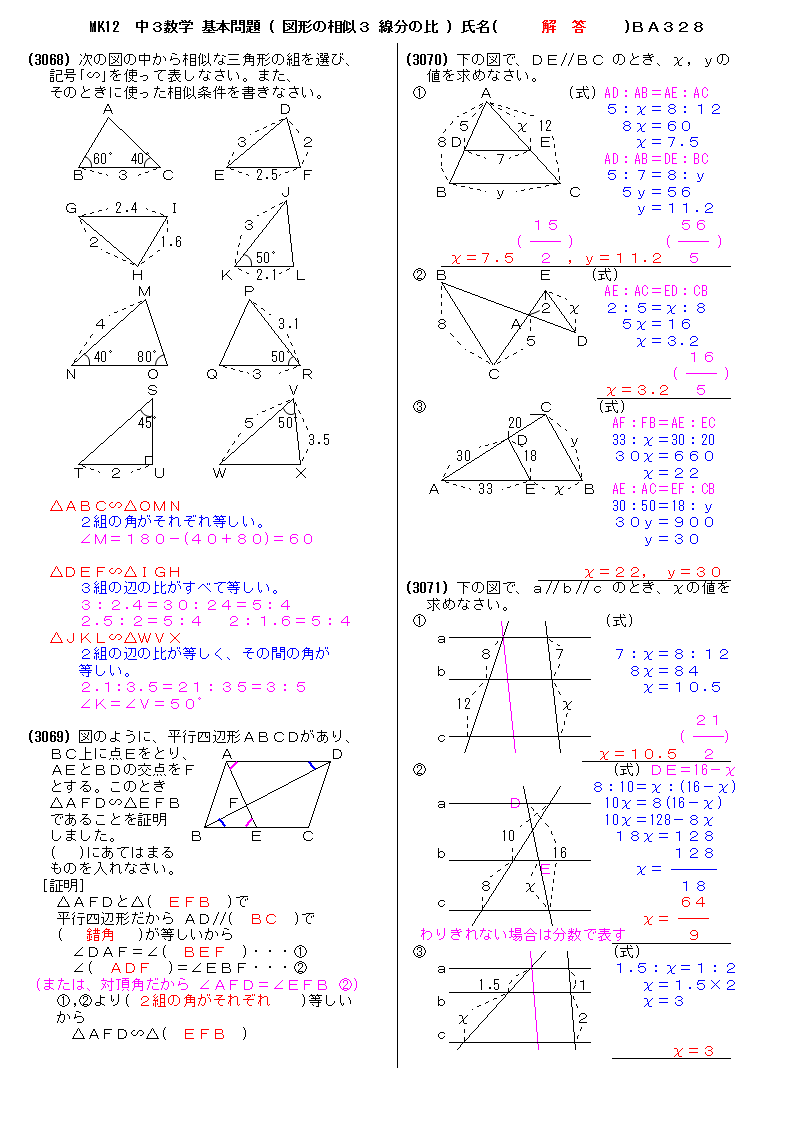



無料 中3数学 基本問題 解答プリント 328 図形の相似3 線分の比



平行線と線分の比 Youtube




相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




中学3年の数学 動画 平行線と線分の比 基本編の問題 19ch



0 件のコメント:
コメントを投稿