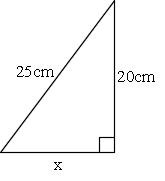
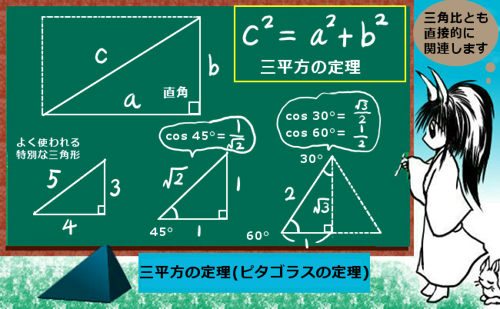
几何课关于三角形你不得不记住的定理:从勾股定理到托勒密定理 直角三角形的两条直角边的平方和等于斜边的平方。 也叫毕达哥拉斯定理。 表达式为a b =c 。 在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。 也叫欧几里德定理。 在RtABC中,∠ACB=90°,CD是斜边AB上的高,则有座標上での2点間の 三平方の定理とは、直角三角形の三辺の長さに関する定理である。 斜辺の2乗は他の2辺の2乗の和に等しくなる。 三角形の三辺をa,b,cとし、斜辺がcとするとc^2=a^2b^2となる。左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64
三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典
直角三角形 三平方の定理 計算
直角三角形 三平方の定理 計算- 三 平方 の 定理 直角 三角形45°:45°:90°の直角三角形 こちらは直角以外の2角が2つとも45°になっている三角形、すなわち直角二等辺三角形です。これは辺の比が1:1:√2になります。在 ABC中, sin²Asin²Bsin²C = 1cos(2A)/2 1cos(2B)/2 1cos(2C)/2( 降幂公式 ) = cos(2A)cos(2B)/21/21/21/2 cos(2C)/2 =cos(AB)cos(AB) 1cos(2C)/2( 和差化积 ) =cos(AB)cos(AB)cos²C( 降幂公式 ) =cosC*cos(AB)cosC*cos(AB)(∠A∠B=180°∠C以及 诱导公式 ) =cosC cos (AB)cos(AB)




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ
直角三角形で最も有名な公式である三平方の定理(ピタゴラスの定理)は中学3年の数学で学習します。 次に、4つある直角三角形のひとつを考えます。 ・正方形の中に内接する正方形を描く。 2点間の距離を求めなさい。勾股定理 直角三角形两直角边(即"勾","股")边长平方和等于斜边(即"弦")边长的平方。也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 。 勾股定理只适用于直角三角形,应用于解决直角三角形中的线段求值问题。三平方の定理とは、直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを cとしたときに、公式 a 2 b 2 = c 2 が成り立つという定理です。ここで、斜辺とは、直角三角形の直角に対する対辺のこと
三平方の定理直角三角形辺の長さ 四平方の定理直角三角錐面の面積 三平方の定理は, 直角三角形において,斜辺の平方は直角をはさむ2辺の平方の和に等しい と表現される. 四平方の定理を同様に表現すると,次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.)三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し
反之,若平面上三角形中两边长的平方和等于第三边边长的平方,则它是直角三角形(直角所对的边是第三边) 定理作用 ⑴勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理。 ⑵勾股定理导致不可通约量的发现,从而深刻揭示了数与量 ①直角三角形的两个锐角互为余角; ②直角三角形斜边上的中线等于斜边的一半; ③直角三角形的两直角边的平方和等于斜边的平方(勾股定理); ④直角三角形中30度 角所对的直角边等于斜边的一半; 直角三角形的判定: 直角三角形边长公式:c²=a²b² ,已知三角形两条直角边的长度 ,可按公式c²=a²b²计算斜边。 直角三角形边长关系 1、两边之和大于第三边 2、直角三角形中两直角边的平方和等于斜边的平方(c²=a²b²) 30度直角三角形边长,30度角所对的直角边是斜边的一半




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
次の直角三角形において,xの長さを求めなさい (1) 日本大百科全書(ニッポニカ) 三平方の定理の用語解説 直角三角形abcが与えられたとき、斜辺bcを1辺とする正方形の面積は、他の2辺ab、acを1辺とする二つの正方形の面積の和に等しい。 三平方の定理(ピタゴラスの定理) 直角三角形において, a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺の二乗」と等しい。 a, b, c a,b,c a,b,c は直角三角形の3辺の長さで, c c c が斜辺です。視覚的証明 初等幾何学 における ピタゴラスの定理 (ピタゴラスのていり、 英 Pythagorean theorem )は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} が成り立つという 等式 の形で述べられる 。 三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげん




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



リンクの図に示すように 長方形の中に直角三角形が2つあります ある程度わかっている寸法をもとに短辺abの長さを求めると どういう値になりますか Quora
下列定理有逆定理的是( )全等三角形的面积相等对顶角相等同角的余角相等直角三角形两条直角边的平方和等于斜边的平方 1年前 5个回答 直角三角形三边关系性质1:直角三角形两直角边的平方和等于斜边的平方性质2:在直角三角形中,两个锐角互余性质3:在直角直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度③利用三角形内角和定理求第三个角 例3在 ABC中,已知 , , ,求b及A 解析由题意得 , , 4、已知三边解三角形 已知三角形的三边a,b,c,解三角形的步骤: ①利用余弦定理求出一个角; ②由正弦定理及 求其他两个角 例4在 ABC中,已知 , , ,求最大角和




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール
已知一个直角三角形的三边的平方和为1800cm2,则斜边长为A30 cmB80 cmC90 cmD1 cm – 新东方在线网络课堂 题目 题型: 单选题 难度: 简单 来源:新东方在线网络课堂 三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います 直角三角形两直角边a、b的平方和等于斜边c的平方。 要点诠释 勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用 1已知直角三角形的两边求第三边, 2已知直角三角形的一边与另两边的关系,求直角三角形的另两边 3利用




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




数学 中3 61 三平方の定理 基本編 Youtube
勾股定理不只是数学家爱好,魅力真大!,驶向胜利的彼岸,勾股定理的逆定理,如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形,已知如图(1),在abc中,ac2bc2=ab2 求证abc是直角三角形,驶向胜利的彼岸,逆定理的证明,证明作rt a。 Pythagorean theorem は直角三角形の3辺の長さの関係を表す 斜辺の長さを c 他の2辺の長さを a b とすると定理は が成り立つという等式の形で述べられる 三平方の定理さんへいほうのていり勾股弦の定理こう 中学直角三角形问题的解决测试点1直角三角形的性质1直角三角形的两个锐角互为补充,可表示为: C90 a B90在直角三角形中,与角30相对的右侧等于斜边的一半。直角三角形斜边上的中心线等于斜边的一半4毕达哥拉斯定理:如果直角三角形的两,新文库网




三平方の定理について考える5 直角三角形の合同条件のひとつ 身勝手な主張




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube
Abに平行な線をo'を通るように引き、 oaの延長との交点をcとする。 数学b2 班 今井 亨 定道 勇斗 谷口 昂平 西川 太朗 二次元での定理を三次元に拡張 1. はじめに 直角三角形で成り立つ三平方の定理(ピタゴラスの定理)というのはかなり有名です。4、勾股定理:直角三角形两直角边a,b的平方和等于斜边c的平方,即a 2 b 2 =c 2 .5直角三角形两直角边a,b的平方和等于斜边c的平方,即a 2 b 2 =c 2 . 由广勾股定理我们可以自然地推导出三角形三边关系对于角的影响.在 ABC中,




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
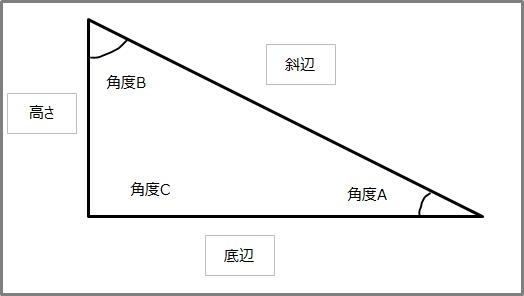



三平方の定理の計算 角度と長さ Nujonoa Blog
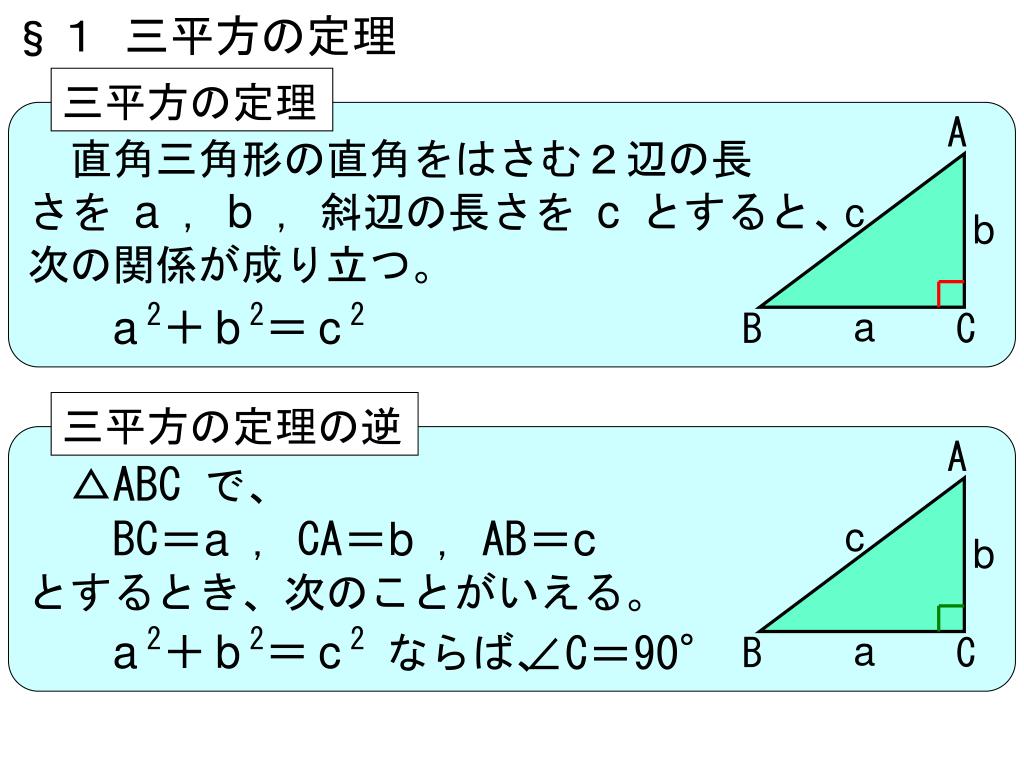



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id



1



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
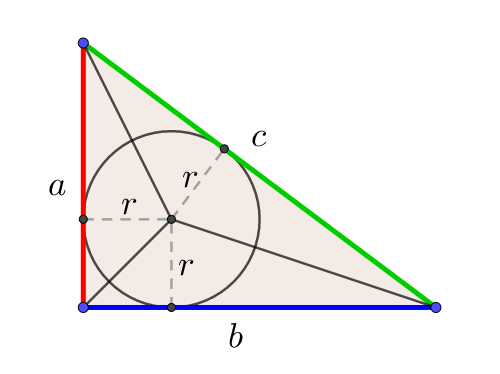



三平方の定理の証明4 直角三角形と内接円 キソカラ
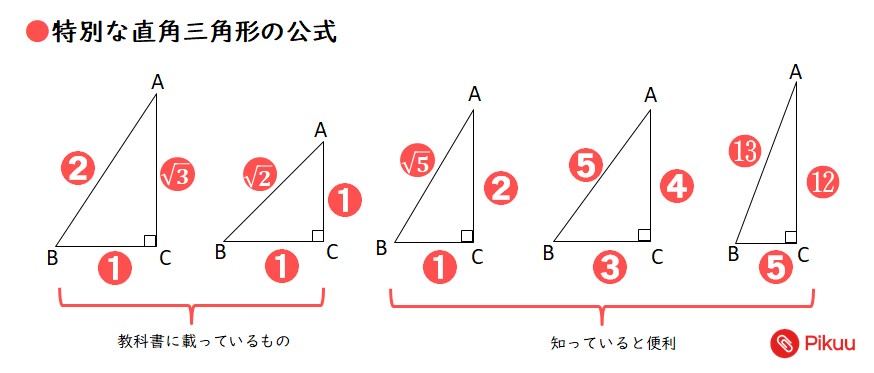



高校入試対策数学 特別な直角三角形を使った問題 Pikuu




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三平方の定理 平面図形 Mp4 On Vimeo




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理 やややさしい数学




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか Yahoo 知恵袋
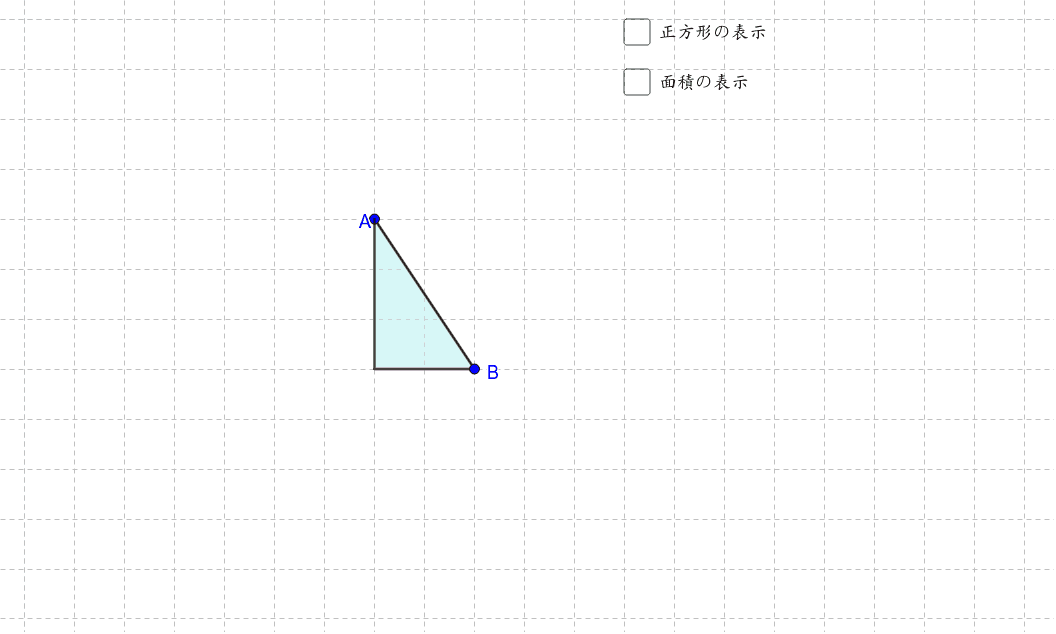



三平方の定理の導入 Geogebra




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
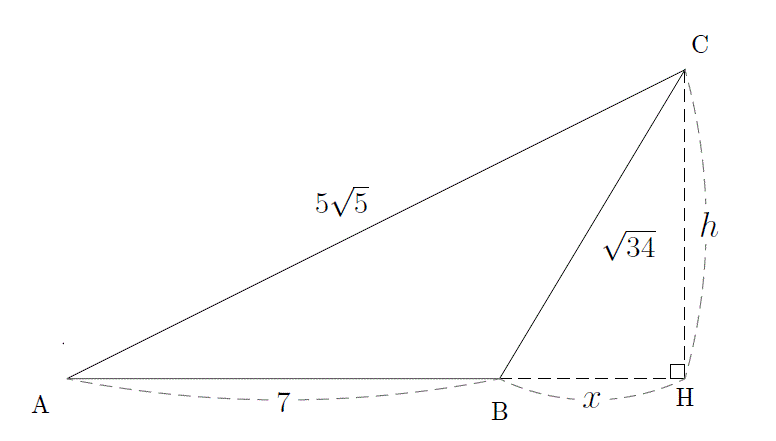



かみのドリル 三平方の定理




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題
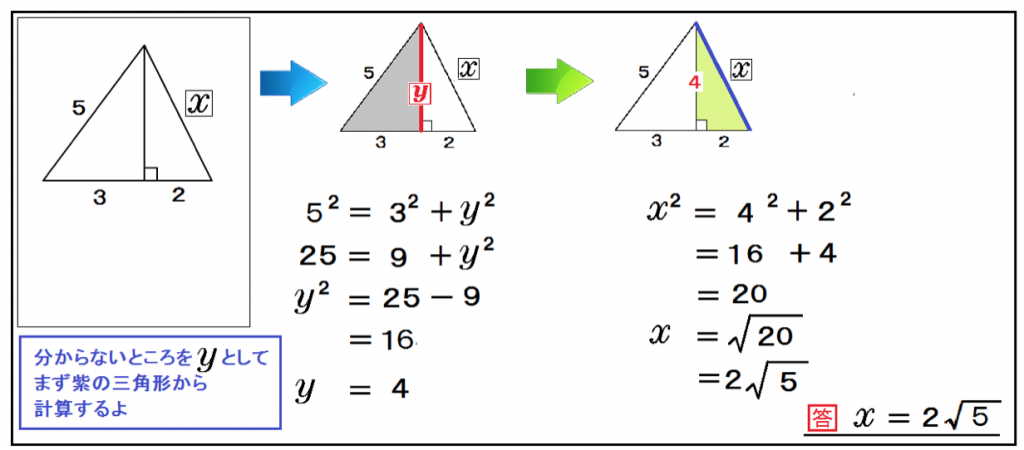



1 1 ルート2 三角形




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs
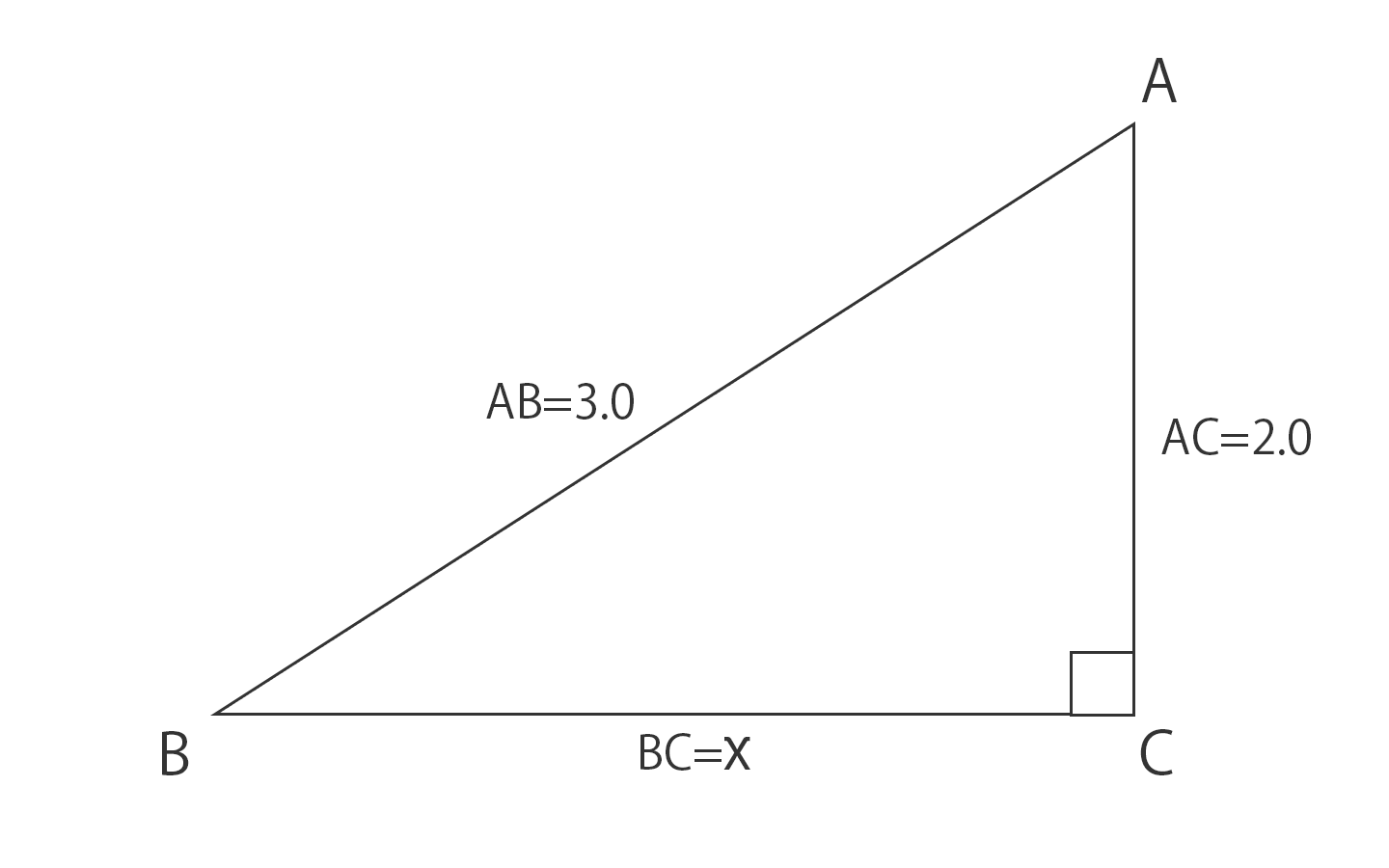



Python 三平方の定理 Unpyside
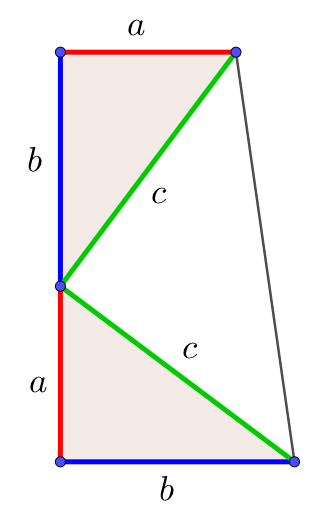



三平方の定理の証明3 大統領の台形 キソカラ



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




三平方の定理の証明と使い方



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




三平方の定理を英語で読んでみる




直角三角形の辺の長さ 合同条件 面積について アタリマエ




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ
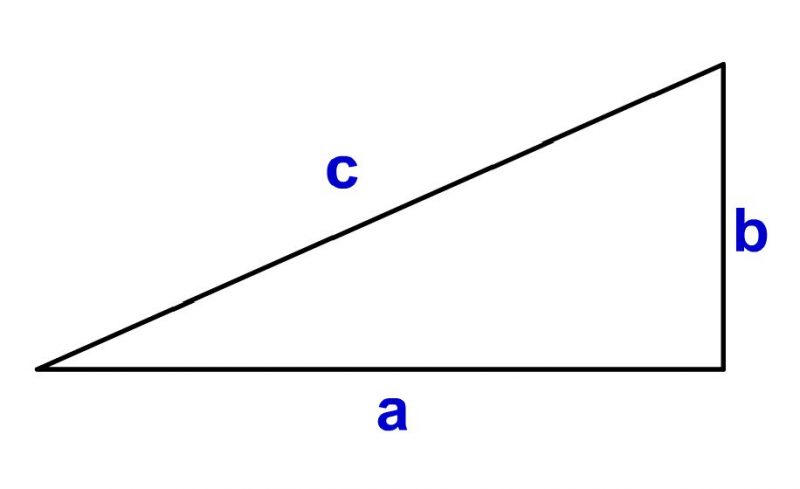



三平方の定理 をシミュレーションで復習しよう 数学入門




三平方の定理 覚えておきたい基本公式を解説 数スタ
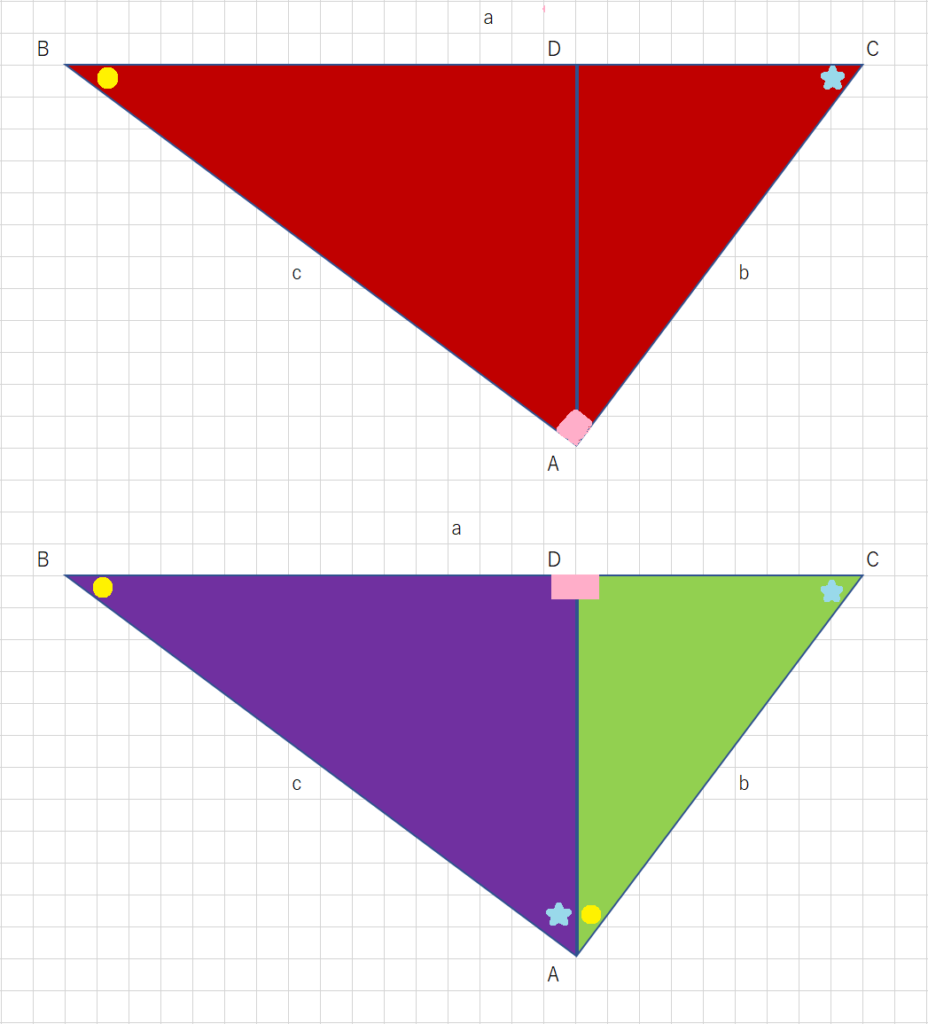



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
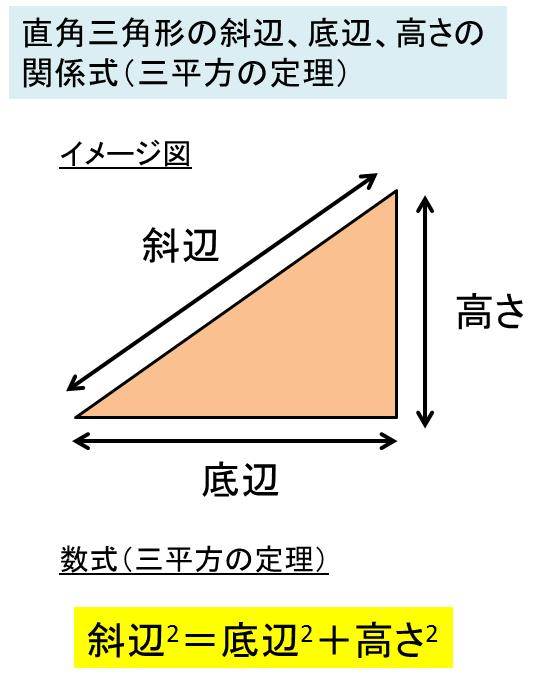



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方



三平方の定理




特別な直角三角形の3辺の比 の問題が分からないんですけど やり方を教えてください Clear



1



1



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




直角三角形 Twitter Search




三平方の定理 おやじさん ネット




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理の応用




三平方の定理で辺を求める Youtube



三平方の定理 スタディーx




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



質問コーナー Discuss Scratch




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




三平方の定理を直角三角形二つで証明 Youtube




三平方の定理の証明と使い方




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




Catatan Tentang 中学数学 三平方の定理のキホン Junior Clear



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




三平方の定理の証明と使い方




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より
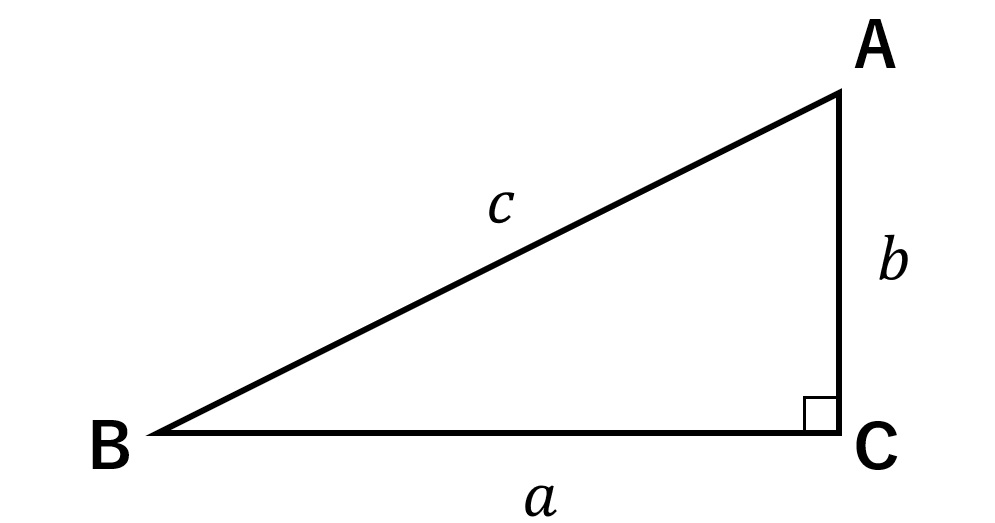



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
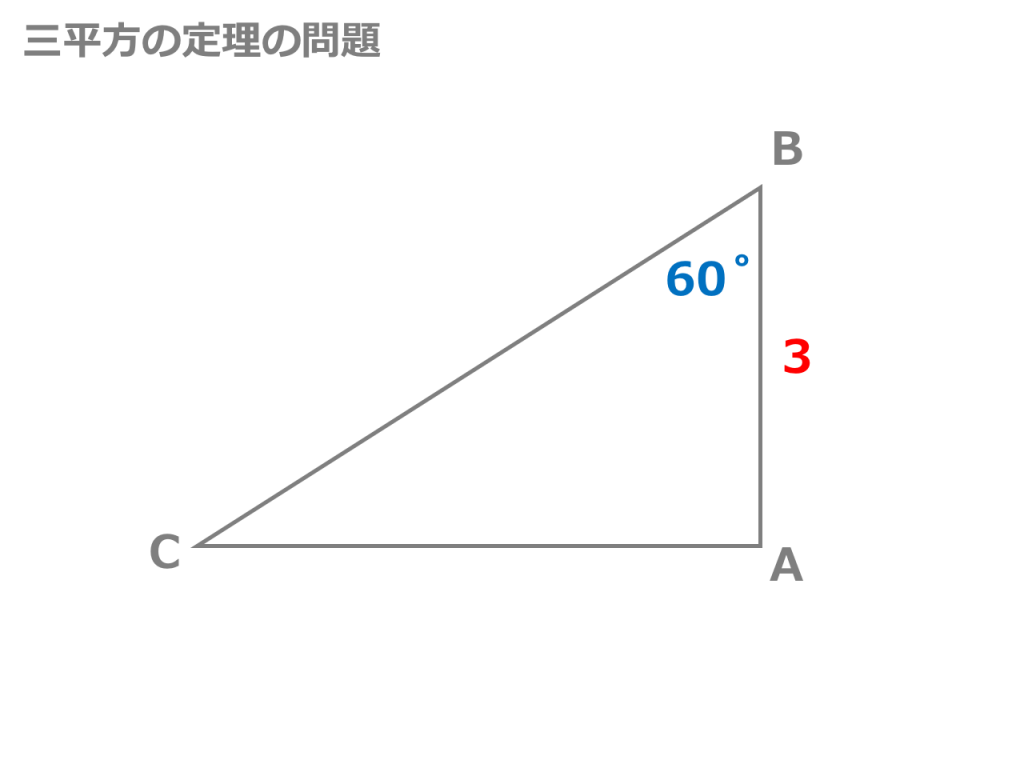



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理 無料で使える中学学習プリント



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau




三平方の定理の逆ってなに どうやって証明するの 数スタ




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー
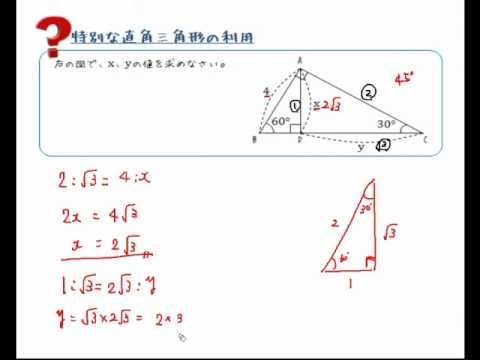



特別な直角三角形の利用 Youtube
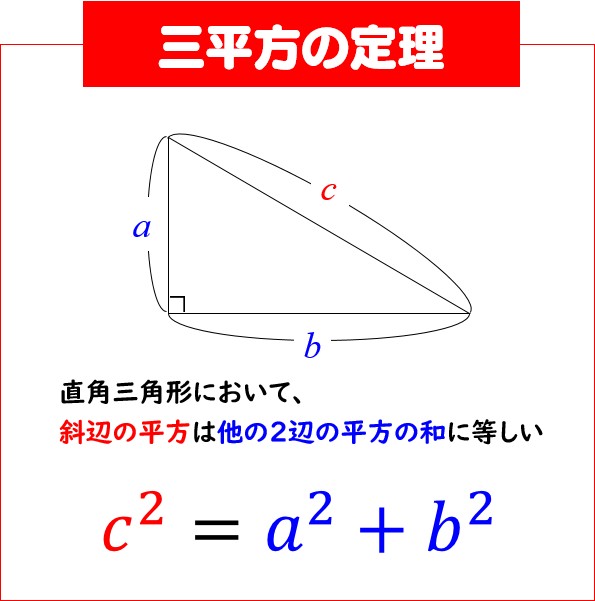



三平方の定理の証明 直感的に分かる図で解説します 数学fun



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




エレガント直角 三角形 の 定理 最高のカラーリングのアイデア




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿