Contents 1 小学4年生 三角・三角定規の勉強を子供に教えていく道のり;2 三角持ち合いのエントリー方法 21 エントリーポイント1ブレイク 22 エントリーポイント2ブレイク後の押し目・戻り目 3 だましを避ける5つの注意点 31 長くて大きな三角形を狙う;三角形を角度によって分けてみましょう。 90°よりも小さい角を 鋭角 、90°よりも大きい角を 鈍角 といいます。
三角形の計算 もう一度やり直しの算数 数学
三角形 種類 英語
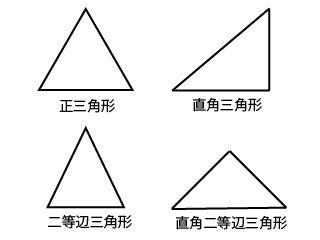
三角形 種類 英語-直角三角形とは、1つの角が90°(直角)な形の三角形のことです。 これが 直角二等辺三角形(ちょっかくにとうへんさんかくけい) です。 直角二等辺三角形とは、 1つの角が直角で、直角を作っている2つの辺が等しい形の三角形 のことです。(1) 三角形は全部で何個できるか答えなさい。 (2) (1)の三角形のうち、合同でない三角形は何種類で、これぞれ何個できるか答えなさい。 2 立方体abcdefghの8個の頂点から3つを選んで三角形をつくる。このとき、 (1) 三角形は全部で何個できるか答えなさい。




标签三角形 跟单网gendan5 Com
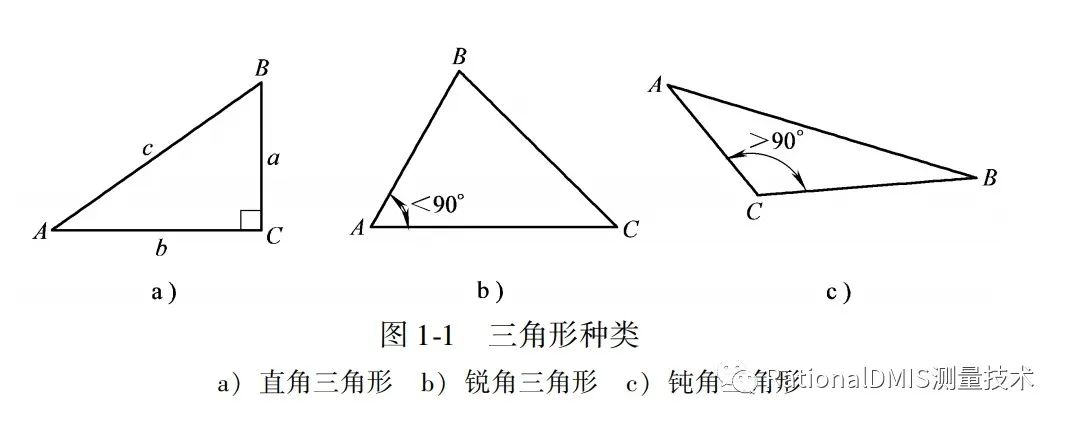
鋭角三角形と鈍角三角形の意味と見分け方 具体例で学ぶ数学 > 図形 > 鋭角三角形と鈍角三角形の意味と見分け方 最終更新日 三角形について、 1番大きい角度が 90 ∘ より小さい→ 鋭角三角形 1番大きい角度が 90 ∘ ぴったり→ 直角三角形 1番三角形の種類 三角形は内角の大きさによって三種類に分けられます。 鋭角三角形 (えいかくさんかっけい) すべての角が90度より小さい三角形です。 直角三角形 (ちょっかくさんかっけい) 90度ちょうどの角がある三角形を直角三角形といいます。 三角形の種類 三角形は内角の大きさによって,$3$ 種類に分けられます. すべての内角が $90°$ 未満のとき,鋭角三角形と言います. 一つの内角がちょうど $90°$ のとき,直角三角形と言います. 一つの内角が $90°$ より大きいとき,鈍角三角形と言います.
三つめは、30度ー60度ー90度の直角三角形です。 この場合、3つの角度はそれぞれ違い、3種類の異なったシンメトリーを作り 、 (30度は12回のパターンを繰り返し60度は6回、90度は4回) それぞれが組み合わされて図5のようなパターンを作るのです。三角スケール 三角スケールは、3面をもつ棒状の定規です。 1面の両側に2つの違う縮尺率の目盛りが入っていて、全部で6種類の寸法が測れます。 主に図面を描くときや、図面をみるときに使用します。 ウチダの三角スケールの特長 1 環境にやさしい入力した3辺の長さから三角形の種類を判別するサンプルプログラムを紹介します。 三角形の種類 三角形 \(ABC\) の 3辺の長さ \(a\)、\(b\)、 \(b\) を入力し 正三角形;
直角三角形 (ちょっかくさんかくけい、 英 right triangle )は、 三角形 の一種である。 三角形の3つの内角のうち、他のどの内角よりも小さくない角に注目したとき、その角が 直角 (90 ° =π/2 rad) に等しい 図形 を指す。 三角形の合同条件 3組の辺が、それぞれ等しい 2組の辺とその間の角が、それぞれ等しい 1組の辺とその両端の角が、それぞれ等しい 合同な図形の対応する 線分の長さ 角の大きさ はそれぞれ等しくなります 先生によって四角形の種類と定義・性質の違い正方形・長方形・平行四辺形・ひし形・台形 管理人 9月 18, 18 / 5月 18, またこれらは包含関係が複雑です。




小学奥数一年级 Doc 文档分享网



Windows游戏编程大师技巧之三角形填充 Cbbbc Csdn博客
7種類の三角形:辺と角度による分類 八月 26, 21 私たちの子供時代、私たちはすべて、学校で数学の授業に出席しなければなりませんでした。三角形の五心とは、 「重心」「内心」「外心」「垂心」「傍心」 の5つの点を指します。 5つの点は、それぞれ定義や性質がまったく異なります。2 小4 三角形を順序良く子供に理解してもらう4つのポイント 21 ;




正六角形三角形小學數學三角形的特性知識點大全 Vnfp



回到开始要画的两个格点三角形 1 10 13六条直角边长分 一家家教育网
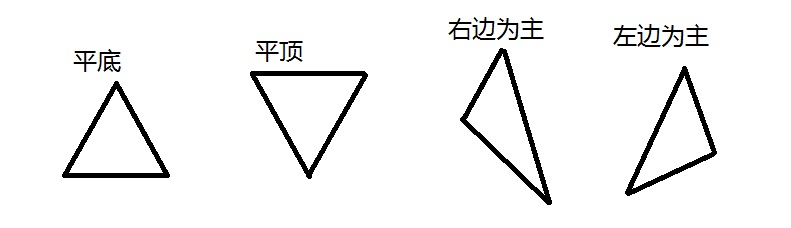
三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。三角地の主なメリットとデメリットは次の通りです。 メリット ・建物の外観が特徴的 三角形の土地の形を活かして、個性的な建物を建てることが可能です。 ・固定資産税が安い三角形と四角形プリント 小学2年生の三角形と四角形プリントです。 こちらは基本的な 図形問題ではありますが、学校でも多くの時間をかけて授業していきます。 まだまだ先の話ですが今後、立方体・四角柱など3次元の図形を理解していく上での 基礎と



三角形种类黄金跌破12关键支撑关注三角形下轨1281水平 妈妈网




鈍角的意思
三角形の種類「二等辺三角形」と「正三角形」 二等辺三角形の性質 ①2つの辺が等しい三角形を、「二等辺三角形」という。 = ②2つの内角が等しい = 三角形は、「二等辺三角形」です。 ③底辺を二等分した直線は、 = で等しい長さになる。正三角形とは3つの辺の長さが等しく、3つの角の大きさが等しい形のことです。 これが 二等辺三角形(にとうへんさんかくけい) です。 二等辺三角形とは、 2つの辺の長さが等しく、2つの角の大きさが等しい形 のことです。三角形 ,又稱三邊形,是由三條 線段 順次首尾相連,或不共線的三點兩兩連接,所組成的一個閉合的平面圖形,是最基本和最少邊的 多邊形 。 一般用大寫英語字母 A {\displaystyle A} 、 B {\displaystyle B} 和 C {\displaystyle C} 為三角形的 頂點 標號;用小寫英語字母
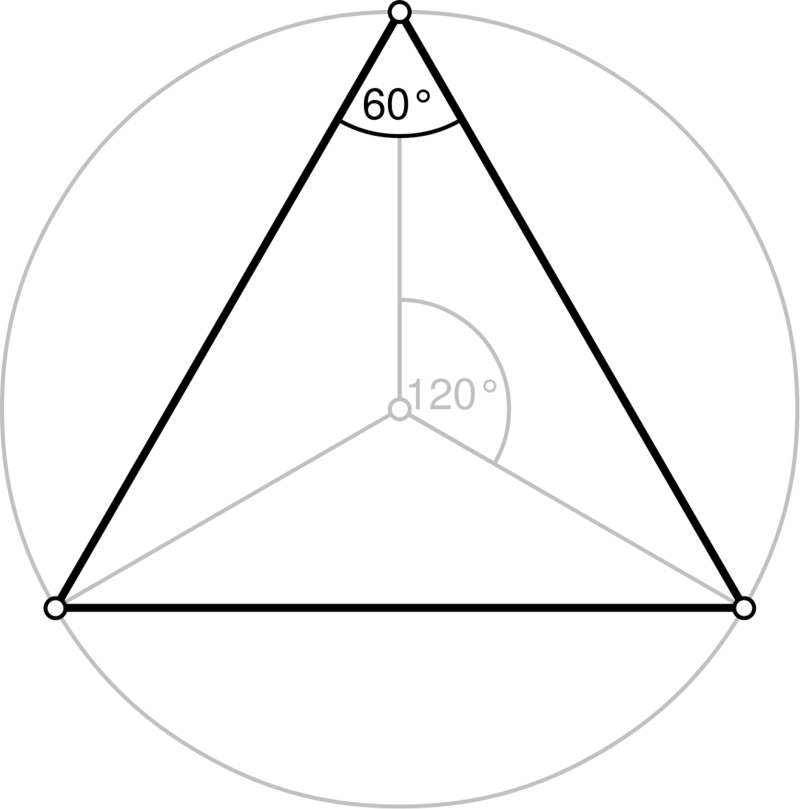



各种三角形的中英文名称对照 英国羽西




四边三角形图片 下面图片中含有几个三角形和四边形 固原市信息网
三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。




多边形分解成三角形算法 台部落




小学生必会的 三角形 简书




三角形变四边形图 三角形具有稳定性 要把四边形变成具有这种性质的图形 至少增加几条线段 固原市信息网



三角形的分类 简书




白色背景上的奶酪三角形种类繁多照片 正版商用图片04ptgz 摄图新视界




几何画板绘制出不同种类的三角形 百度经验



直角 鋭角 鈍角三角形の判定法 思考力を鍛える数学




如何给三角形分类 9 步骤
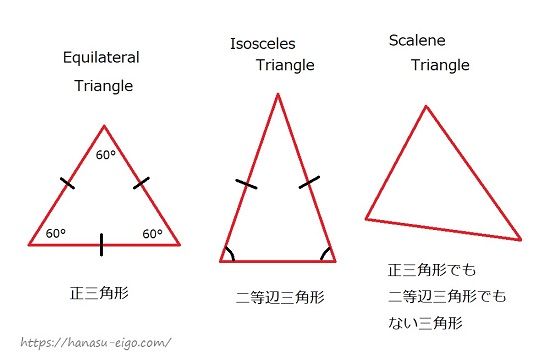



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語
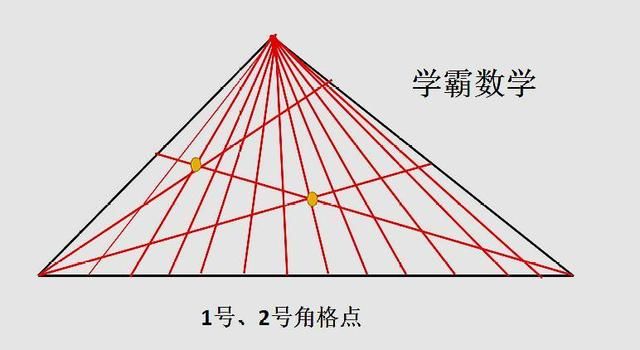



等腰三角形的内心和外心



歡迎蒞臨培基小學網頁




辨認三角形的種類小學三年級數學科 Ppt Download



3年算数三角形教え方のポイント




三角形の計算 もう一度やり直しの算数 数学



三角形有哪些种类图片第1页 驾考预约大全




微博搜索



掌握这些方法 初中数学相似三角形全等三角形证明题都能得满分 初中数学 学习资料大全 免费学习资源下载



解直角三角形计算方法 北京爱智康




特殊三角形 搜狗百科




Java题目集总结 Mbe25a607的博客 51cto博客



1



三角形种类飞行表12点位上的小三角形是什么意思 尚书坊



三角形的种类8种图片 万图壁纸网



Q Tbn And9gct5sdoypltyoboe5xz6xepaqs4jg8baqrmn9fzoq1pq1gafso1b Usqp Cau
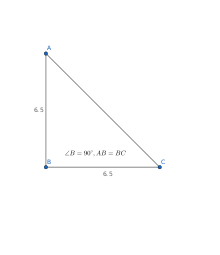



三角形 维基百科 自由的百科全书




全等三角形 维基百科 自由的百科全书



三角形有哪些种类图片第1页 驾考预约大全
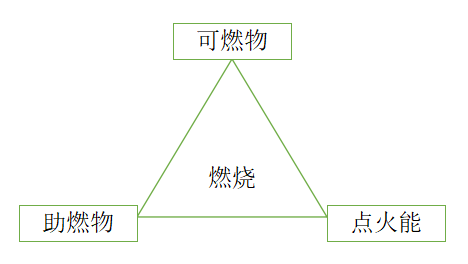



火灾研究基础 燃烧与传热 消防科普2 知乎




三角形の種類を判定しよう 電験3種web
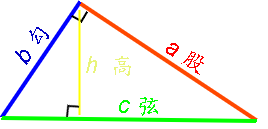



三角形 维基百科 自由的百科全书




區塊鏈種類與不可能三角 三角難題的抉擇 桑幣知識




凸多边形的三角形剖分种类问题 桐小目的秘密基地 程序员宅基地 凸多边形的三角形剖分 程序员宅基地



9 9 24跟三角形聊天 三年級 欣心潛能教學中心 痞客邦




高中數學重難點歸納 解三角形常考題型有三種類型 每日頭條




三角形画像 三角形四角形画像
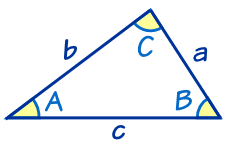



解三角形
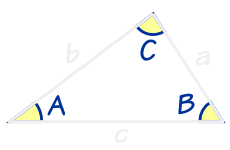



解三角形




三角形分类 视频 三角形 可汗学院




翻轉學習影片 國中 數學 三角形相似性質 三角形相似性質 a Sas Sss




二等辺三角形や直角三角形って英語で何て言うの 三角形の種類について 40代 50代 60代 シニア 初心者からやり直し英会話 英語学習法



1 下图是由边长都是1的小三角形组成 数一数图中三角形的个数 2 根据上表中的数据完成下面的统计 Cc搜题 中小学课程辅导
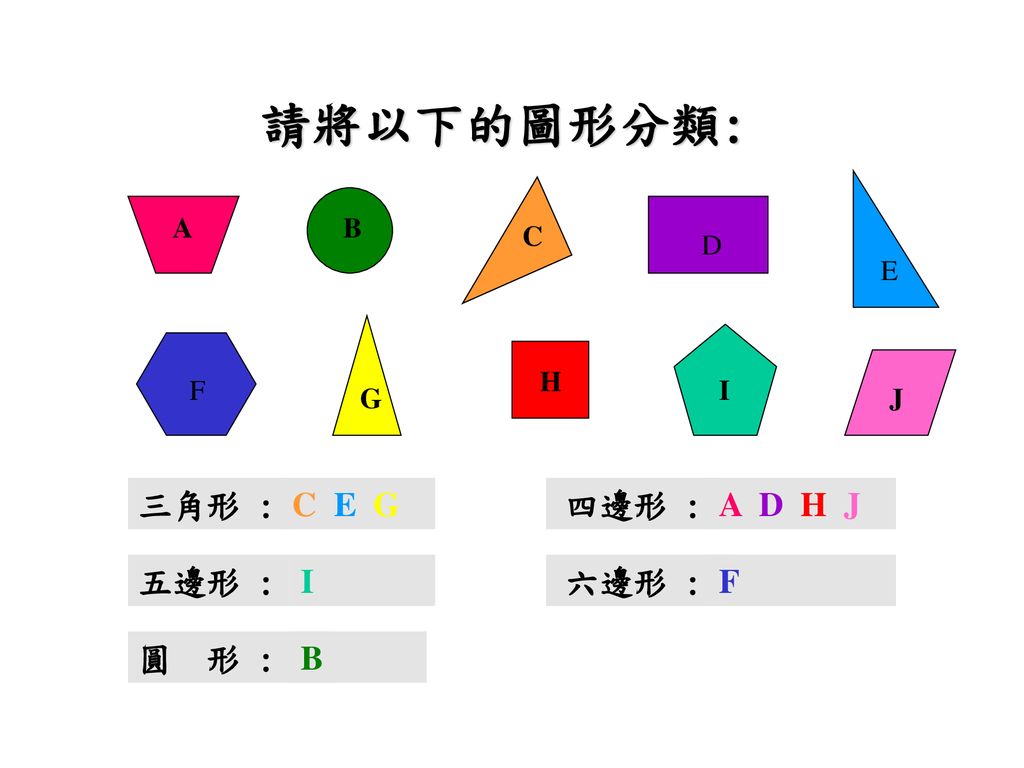



辨認三角形的種類小學三年級數學科 Ppt Download



三角形有几种类型图片 搜狗图片搜索




三角形指示牌价格 三角形指示牌图片 星期三



Q Tbn And9gcs W8527agmiyafsa2s0kpwr16uavujwuhty B15ri Usqp Cau



基于边和角度的三角形有哪些不同类型 定义所有类型 教育小本子




水彩図形 丸 三角 四角 星 ハート 7種類セット Wall Mural Pp7



三角形 尚书坊




有关三角形 不同種類的 事實的免费素材图片




三角形種類
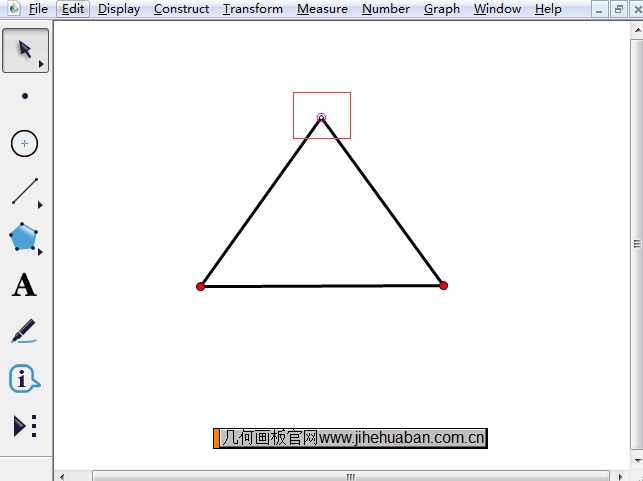



用几何画板快速画出不同种类的三角形




免費先修課程
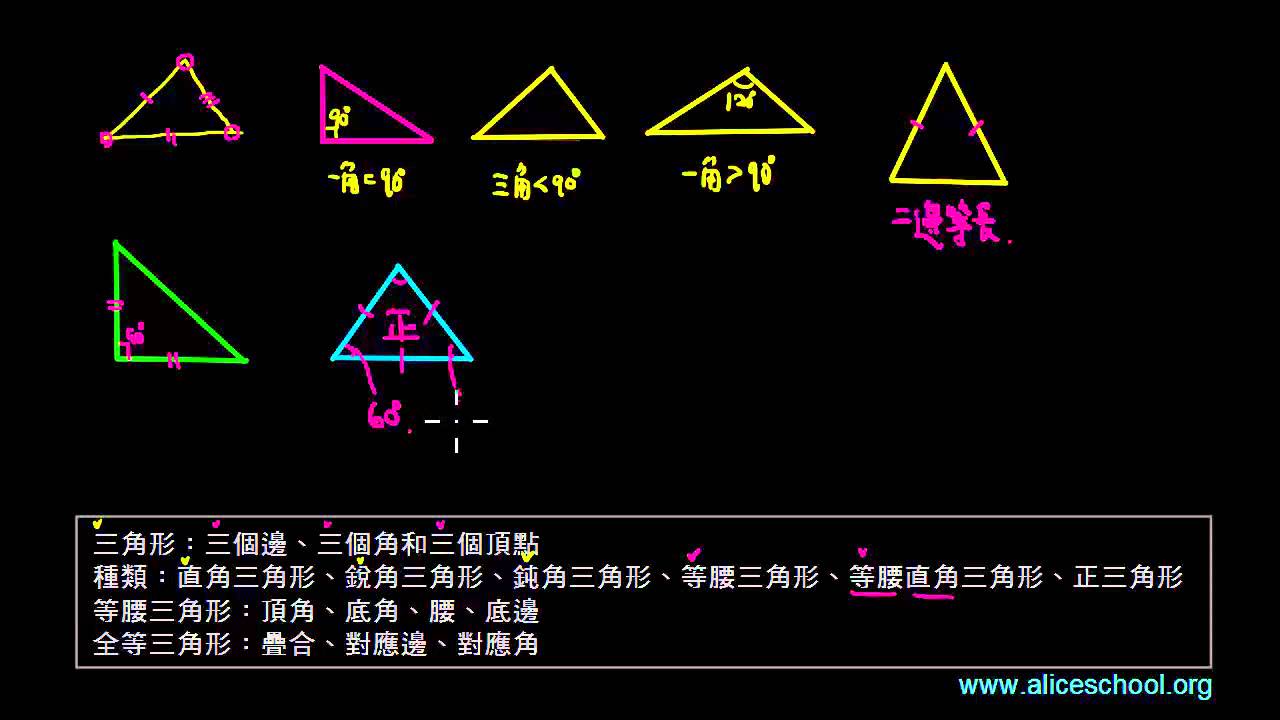



四年級十分鐘數學 三角形 Youtube




三角形 膨大なページ数 Wiki



三角形有几种图片三角形分几种 我有车
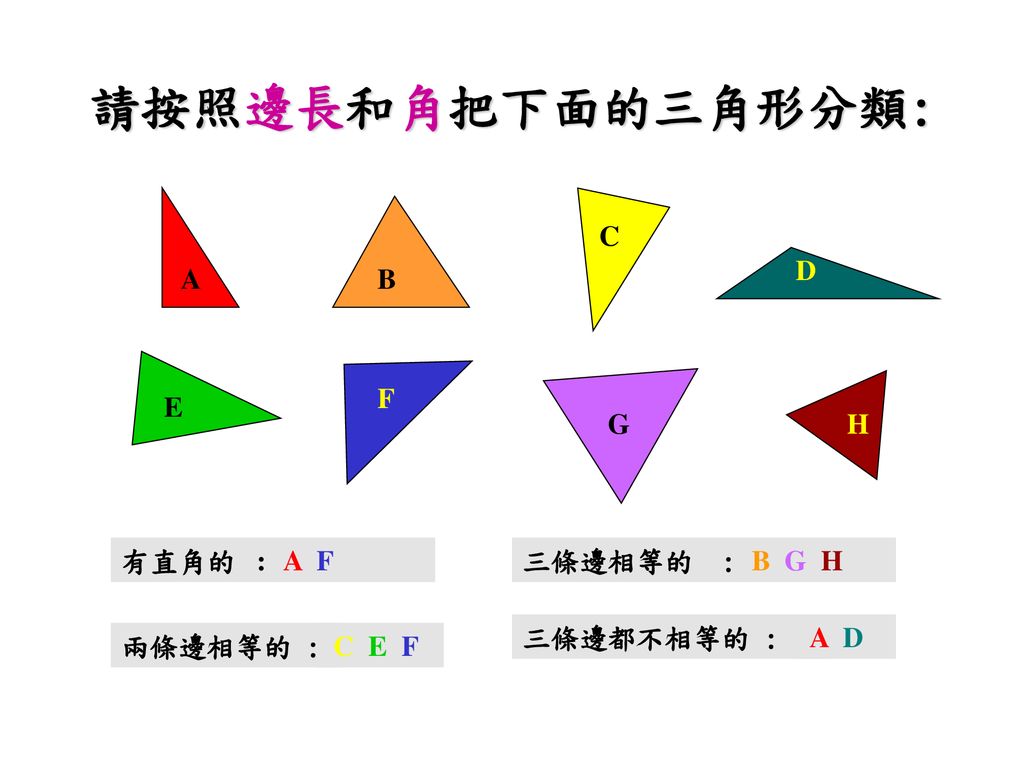



辨認三角形的種類小學三年級數學科 Ppt Download
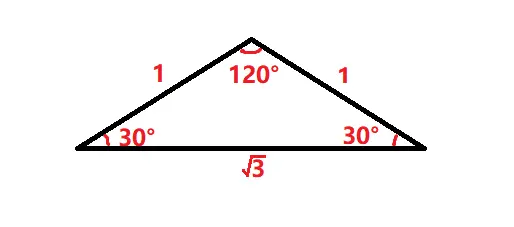



初等数学 三角形 一 三角形的种类 哔哩哔哩
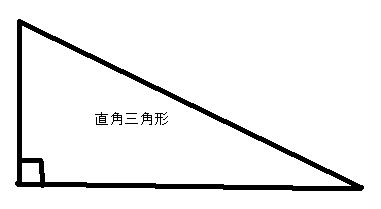



三角形の種類 算数勉強会 小学 楽天ブログ




文具尺是什么材料制作的有哪些种类 品牌百科 品牌网




吳崢 台北市副發言人柯昱安昨天在 年代向錢看 上解釋柯文哲近日批評蔡英文 親美抗中 戰略路線錯誤背後的戰略觀 在網 Facebook



三角形數控車刀片tnmg不銹鋼外圓車床合金刀粒硬鋼件車刀頭 蝦皮購物




二个三角形可以拼成什么图形 两个大小完全相同的三角形可以拼成一个什么图形 三人行教育网 Www 3rxing Org




初等数学 三角形 一 三角形的种类 哔哩哔哩
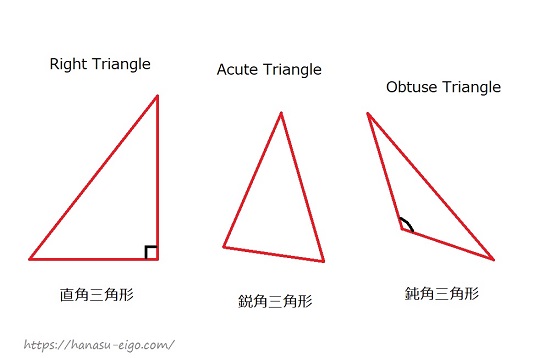



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語




哪種三角形 Slobo




Housida 墙贴check砧纸图案 正三角形4色 各12张共计48张bws 434 ハウスホールドジャパン 价格报价图片




等边三角形 新人首单立减十元 21年8月 淘宝海外




S 8 8 S06 能理解直角三角形 銳角三角形 鈍角三角形 等腰三角形 正三角形 等腰直角三角形 Youtube



1
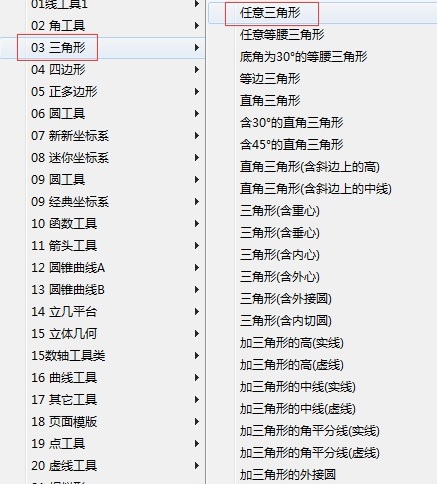



用几何画板快速画出不同种类的三角形



Msdn画圆弧函数 三角函数常识 Weixin 的博客 Csdn博客




技术 图计算的种类和应用场景 知乎




如何给三角形分类 9 步骤




四邊形種類四邊形 Zilhc



非平凡的镜像相似性 科普之友



悟空问答 三角形画辅助线这一块学得不好 怎么办 3个回答




多邊形分解成三角形算法 台部落
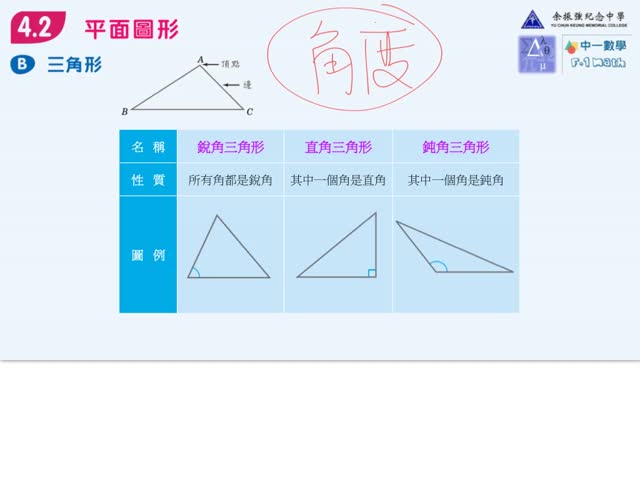



Ch 4 2ab 平面圖形 圓 三角形的種類



三角形按角分类 课堂教学实录 杂志论文 江苏教育研究
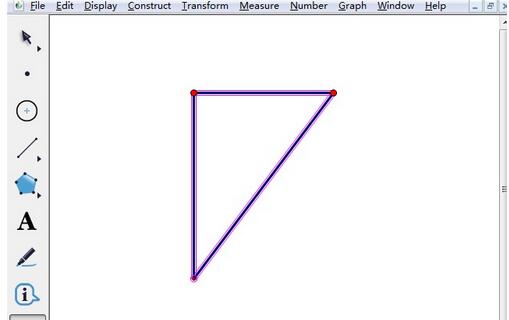



如何使用几何画板绘制任意三角形 佩琪手游网



三角形有哪些种类图片 万图壁纸网




104 根据边和角的类型给三角形分类 Youtube
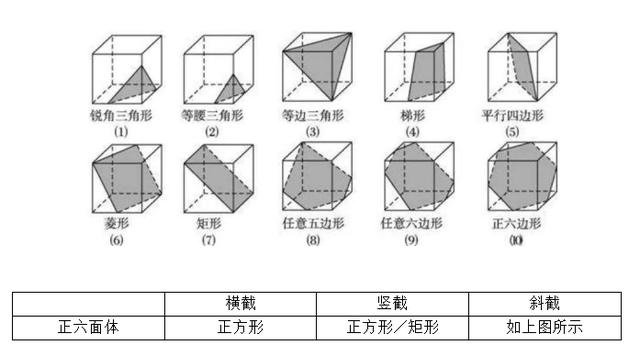



掌握这些知识点再也不怕立体截面图形题了
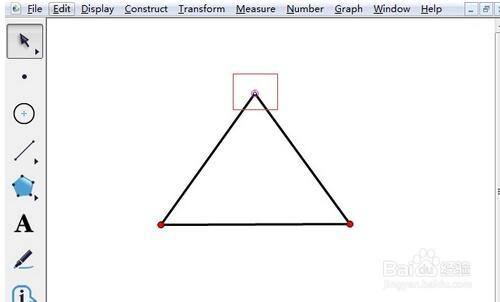



几何画板绘制出不同种类的三角形 百度经验



悟空问答 怎样解决孩子在求三角形和梯形面积时总忘记除以2 小小思维家的回答 0赞



北师大版四年级下册 三角形的分类 Ppt课件2 最新 沃文网wodocx Com




不同的三角形flashcards Quizlet




圖形摺疊中的線段長度真難求 掌握兩種類型一個思想不用愁 每日頭條




标签三角形 跟单网gendan5 Com



2




三角形魔方书目 三角形魔方作品 京东图书




Multicolor 三角形 圖案 針對 粉紅背景種類最齊全的圖像 Ph0 142 Fotosearch




三角形內接矩形 三角形內接矩形的定義 三角形內接矩形的種類 三角形內接矩形的最大面 中文百科全書



三角形有哪些种类图片第1页 驾考预约大全



三角形的分类课件2 人教版小学数学四年级下册课件 小学课件 中国儿童资源网



歡迎蒞臨培基小學網頁



0 件のコメント:
コメントを投稿