円に内接してる、四角形abcdにおいて、ab=5 bc=3 ∠abc=1°である この四角形の面積の最大値を求めよという問題の解説で理解出来ないのがあります 画像が解説なのですが、対角線acに下ろした垂線の長さが最大の時が面積も最大になる。実践記録算数5年 1.単元名 「円」 2.指導によせて <単元観> 円の面積についての一般的な指導の流れは次のようなものである。 (1) 円に内接する正方形をかき,半径×半径の2倍よりも面積は大きいと推測するということは、楕円に内接する四角形についても、面積は伸縮変換に対応するので、伸縮 した円に内接する正方形を元の伸縮率にした四角形が最大面積を与えるということになりま すね。 S(H)さんが上記の問題を考察されました。(平成24年2月12日付け
中三です 下の図のように 円に内接する四角形abcdがあり 対角線ac Yahoo 知恵袋
円に内接する四角形 面積 対角線
円に内接する四角形 面積 対角線- ブラーマグプタの公式は, 円に内接する四角形の4辺の長さが分かっている場合にその面積を求める公式です 数学のカ 現役京大生が数学の定理・公式の証明や入試問題の解説をするブログ>θ は長軸半径 a、短軸半径 bを半径とする円においての角度で なるほど。そうですね。 半径aの円に内接する四角形の最大は正方形であることを示すなら、asinθ・acosθ=a^2 sin2θが最大となるときで問題ないですが、楕円で円と同じことをやってもだめですね。
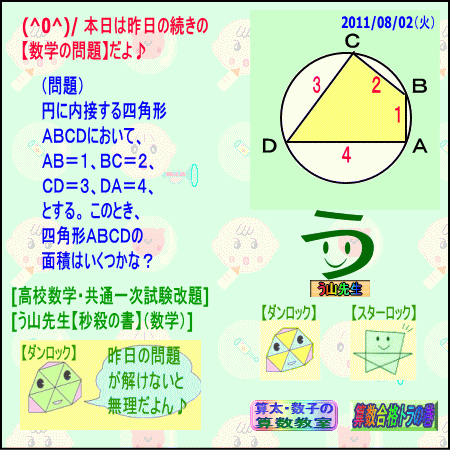



内接四角形 11年8月2日ブログ問題 カンブリア アカデミー 高等部 Byオルドビスキー博士
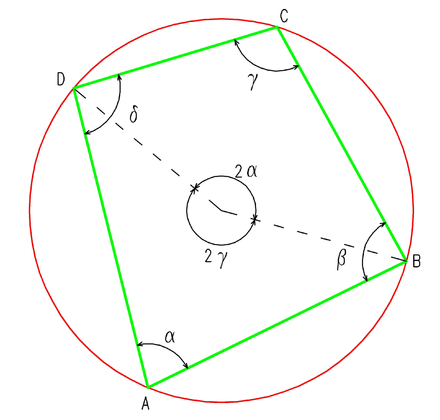
定円に内接する四角形abcdがある。a~dを動かしてabcdの面積を最大にせよ。 , 定円に内接する四角形abcdがある。a~dを動かしてabcdの周を最大にせよ。ただし辺が交差してはいけない。 , 定円に内接する三角形abcがある。a~dを動かしてabcの面積を最大にせよ。初等幾何学における共円四辺形(きょうえんしへんけい、英 concyclic quadrilateral, cyclic quadrilateral )または円に内接する四辺形あるいは(円)内接四辺形 (inscribed quadrilateral) は、そのすべての頂点が「同一円周上にある」ような四辺形を言う。 このとき、すべての頂点が共有する円$3$ 辺の長さと面積が整数であるような三角形を「ヘロンの三角形」(Heronian triangle)と呼び, そのうち $3$ 辺の長さが連続する整数であるものを「ブラーマグプタの三角形」(Brahmagupta triangle)と呼ぶ 本問の結果により,「ブラーマグプタの三角形」の $2$ 番目に
形{b, c, d} の面積を表すため,式(35) は円内接五角形を四角形十三角形に分割した場合でも成立する. 円内接七角形の分割への適用 面積Sの円内接七角形{a1, a2, a3, a4, a5, aか妬}を2本の対角四角形abcdは、acに補助線を引くことで abcと acdに2分することができ、それぞれの三角形の面積を求めて足し合わせることで、四角形の面積を求めることができます。 こう考えたら、少しは問題を解ける気がしませんか?極座標における円の方程式の一般形と例題 円に内接する四角形の面積を求める公式 正八面体の体積、表面積、外接球の半径、内接球の半径 正四面体の高さと体積の求め方 図形の面積を求める公式たち19個 円の面積を積分で計算する2通りの方法 楕円に
この円に内接する四角形の面積公式(裏技)は,\ {4辺が整数}の場合に特に有効である 4辺の中に無理数があったりしてsが複雑な値になる場合,\ 三角比で求めた方が楽になる 裏技ということは記述試験での無断使用は推奨されないということである4 内接円を扱った問題を解いてみよう 41 問1(1)の解答・解説;3 三角形と円に内接する四角形 31 四角形は三角形2つぶん;
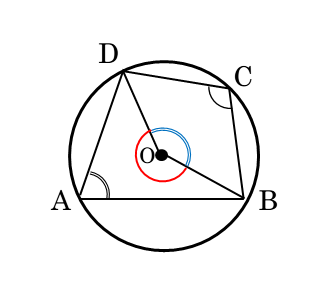



図形と計量 正弦定理 余弦定理 面積への応用について 日々是鍛錬 ひびこれたんれん




高校数学 数 円に内接する四角形abcdの対角線の長さと面積 Youtube
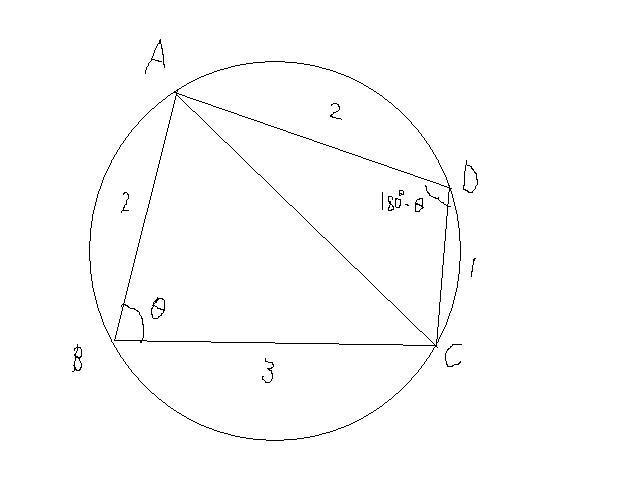
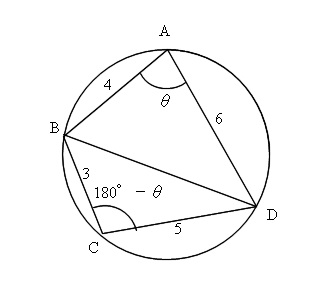
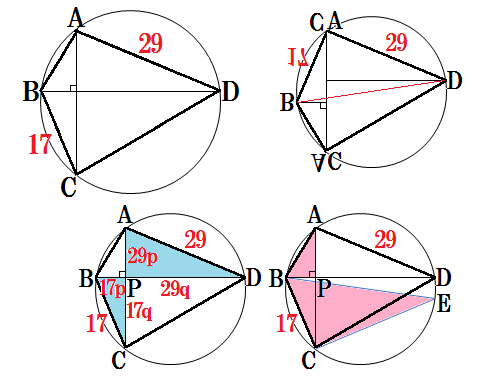
問 円oに内接する四角形abcdが ab=2,bc=3,cd=1,\angle abc =60°を満たしている。(1) 円oの半径rを求めよ。(2) 四角形abcdの面積sを求めよ。かったるい2 円に内接する四角形を対角線で4 分割してできる4 個の三角形について 円 or に内接する四角形abcdの面積を s ,四角形abcdの対角\(\angle\mbox{ABC} = \theta\) とおくと,四角形 \(\mbox{ABCD}\) が円に内接するので, \(\angle\mbox{ADC} = 180^{\circ} \theta\) となります



1




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
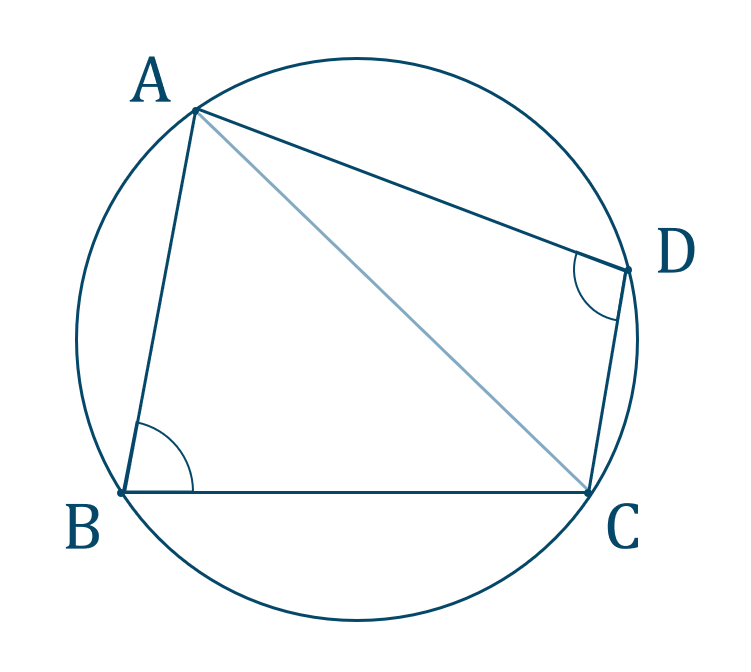
ブラーマグプタの公式 (ブラーマグプタのこうしき、 英 Brahmagupta's formula )とは、 円に内接 する 四角形 の四辺の長さからその四角形の 面積 を求める 公式 である。円に内接する四角形 円に内接する四角形の性質は、高校数学の範囲ですが、中学生も知っておくと便利です。 それに、中学生が学習してもなんなく習得できます。簡単です。 例1 下の図で、角 \(x\) を求めなさい。 解答 円に 四角形を 2 つの三角形に分けて 、三角形の面積の公式「 \displaystyle S = \frac {1} {2} bc \sin \mathrm {A} 」で面積を表します。 ヘロンの公式の証明と同様、三角比の相互関係と余弦定理を用いて三角比を辺の長さで表現すれば証明できます。




円に内接する四角形の面積をサインを使って求める問題 数学i By ふぇるまー マナペディア




原田 浩明 En Twitter Sサクシード321 円に内接する四角形の面積 対角のcosで対角線の長さを2通りで表しcosを求めてsinにして 面積を求める 数学i 三角比
円に内接する四角形の面積 内接四角形の性質xy=180°と△ABDの面積が ad sin x、△BCDの面積が bc sin yとなることを利用し、また余弦定理を使ってBD 2 を2通りに表わすと、全体の面積の式からsin x、sin yなどを消去することができます。 三角比で円に内接する四角形の面積を求める手順 11 Step1 対角線をひき、余弦定理を使う 12 Step2 2つの三角形の面積の和を求める 13 ブラーマグプタの公式を使う 2 問題編四角形の面積を求めてみようつまり, 向かい合う内角の和が 180^ {\circ} 180∘ である四角形は円に内接します。 また,性質1は「外角」を使って表現されることも多いです。 性質1'




三角比を使って円に内接する四角形の辺の長さ 面積を求める方法 数学i By Okボーイ マナペディア




Abcd Ab3 2 Descubre Como Resolverlo En Qanda
円に内接している四角形の面積の最大値について 円に内接してる、四角形abcdにおいて、ab=5 bc=3 ∠abc=1°である この四角形の面積の最大値を求めよという問題の解説で理解出来ないのがあります 画像が解説なのですが、対角線acに下ろした垂線の長さが最大の時が面積も最大に第76問 内接する三角形 図形ドリル 第60問 立方体の表面積 図形ドリル 第51問 正方形とおうぎ形 図形ドリル 第94問 台形と内接円 図形ドリル 第133問 おうぎ形と直角三角形 図形ドリル 第2問 半円と正方形と3:4:5 円に内接する四角形の面積 円に内接する四角形の 対角の和は180° となる。 面積を求めるときは対角線で2つの三角形に分ける。 円に内接する四角形abcdがある。ab=6, bc=13, cd=9, da=6である。 この四角形abcdの面積を求めよ。 対角線acで abcと adcに分けて考える。
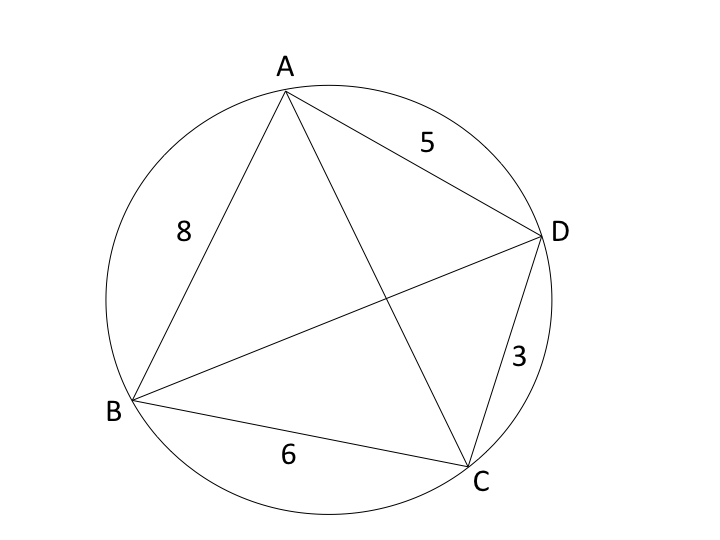



3分で分かる トレミーの定理とその使い方 合格サプリ




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
22 円内接五角形に対する統合公式 既知の方法 6 5 2 により,半径公式 (2,922項) は既に求められているものとする.(1690) などが,最終的な展開形までは至らないまでも,「直径に関する14 次 方程式」 を正しく導いている 3 和算家の方法を数式処理で実行するには,以下のように定式化する.まず,図1 と同様に,円内接五角 形を3 つの三角形に分割し,対角線の長さを円に内接する四角形の性質 作成者 飛田 健次 トピック 円, 四角形 円に内接する四角形の性質 関連トピック 面積;




円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su




円に内接する四角形abcdにおいてab 2 4 Cd 3 Da 2とするとき Clear
2 ユークリッド内接多角形のとき 三角形や円に内接する四角形は辺の長さの四則演算とべき根を使って面積を表す公式が知られている 円に内接する三角形ABC の面積S はHeron の公式として知られていてs = a b c 2 とすると S = √ s(s a)(s b)(s c) と表せる星型多角形 Wikipedia 三角形・四角形では辺の延長上に交点が現れないため、その図形自身のみが星型多角形となる。 五角形 ・ 六角形 では交点が一回現れ、それぞれ 五芒星 ・ 六芒星 と呼ばれる。 正三角形の一辺の長さを a とすると、面積 S は と表さ 16年10月23日 年5月15日 基本三角比と円に内接する四角形 では、円に内接する四角形の「向かい合う2つの内角の和が180度になる」ことを利用した三角比の問題を考えました。 ここでも、それに関連した問題を考えます。 少し難易度は上がります。



円に内接する四角形の対角線の分割比画像のように 円に内接する四角 Yahoo 知恵袋



円に内接する四角形abcdにおいて 2つの対角線ac の交点を Yahoo 知恵袋



円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する
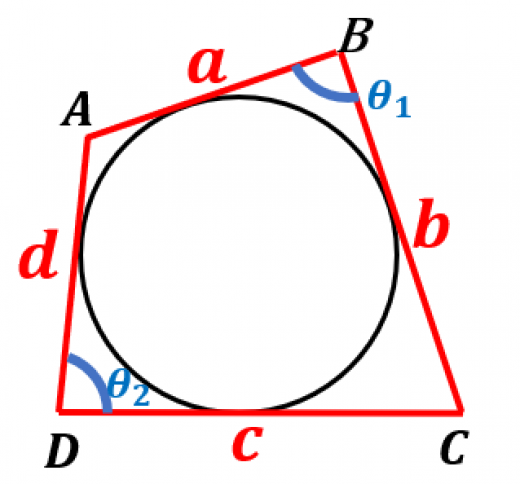



円に外接する四角形の重要な2つの性質 高校数学の美しい物語




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月




数1の円に内接する四角形の問題です よろしくお願いします Clear



東北学院大学 文系 16年問題1 Suugaku Jp
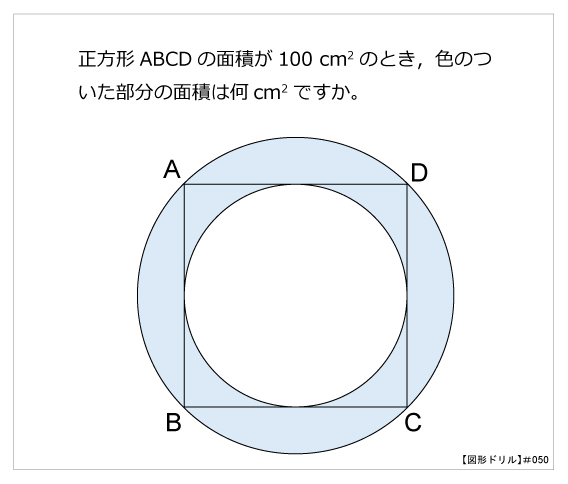



図形ドリル 第50問 内接円と外接円 算数星人のweb問題集 中学受験算数の問題に挑戦



円に内接する四角形 苦手な数学を簡単に




円に内接する四角形2 トレミーの定理 身勝手な主張



Www Junten Ed Jp Contents Wp Content Uploads 13 04 90f3dca3ecefd1db Pdf




円に内接する四角形の面積を四辺の長さで表す 2019年度前期日程の京都府立大学生命環境学部の入試 身勝手な主張



中三です 下の図のように 円に内接する四角形abcdがあり 対角線ac Yahoo 知恵袋



七五三 三角形から円に内接する四角形へ




数 A 円に内接する四角形は対角を見ろ 岡山医学科進学塾のブログ
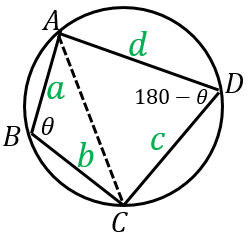



円に内接する四角形の面積を求める公式 具体例で学ぶ数学



共円四辺形 Wikiwand
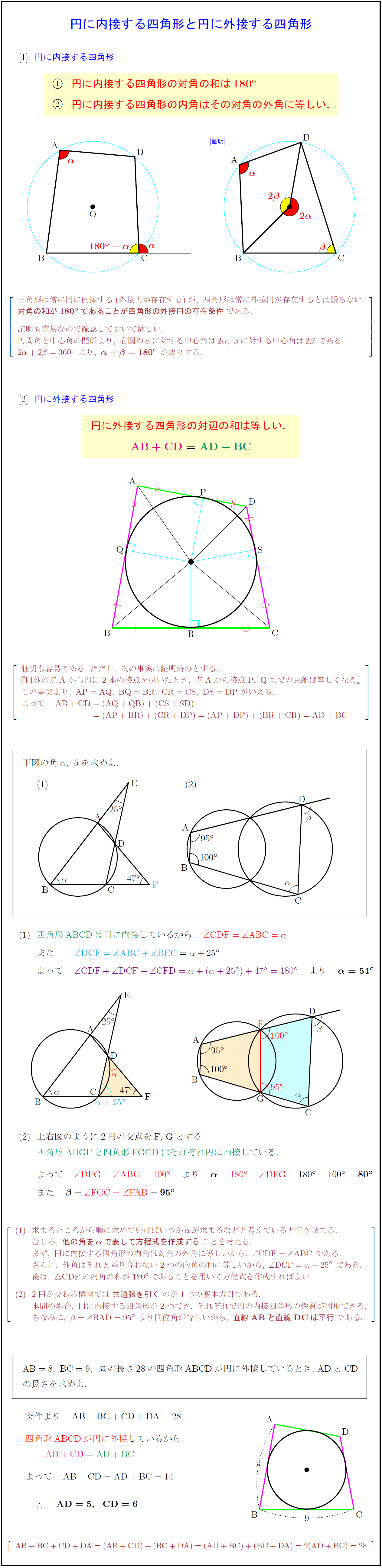



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月



円に内接 外接する多角形



円に内接する四角形abcdについて 対角線acの長さ 辺ad Yahoo 知恵袋




高校数学 円に内接する四角形の対角線の長さと面積 受験の月




円に内接する四角形の面積 数学i 三角比 Youtube



早大理工数学 09年 4




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




標準 三角比と円に内接する四角形 なかけんの数学ノート




高校数学 三角比 円に内接する四角形の面積求め方まとめと問題




円に内接する四角形の面積を求めるブラーマグブタの公式 2017年度前期日程の大阪教育大学教育学部入試問題 身勝手な主張



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




3 Sinabc Dfracbarsqrtd Descubre Como Resolverlo En Qanda



広がる四角形 Nano25の数学学習ソフトウェア



数学 円に内接する四角形のやり方とコツ ページ 2 教科書より詳しい高校数学




数 A 円に内接する四角形は対角を見ろ 岡山医学科進学塾のブログ




基本 三角比と円に内接する四角形 なかけんの数学ノート



円に内接する四角形の問題です 大学入試数学問題の解説 解答



円に内接する四角形の面積の求め方と定理の使い方




1 円に内接する四角形の様々な性質
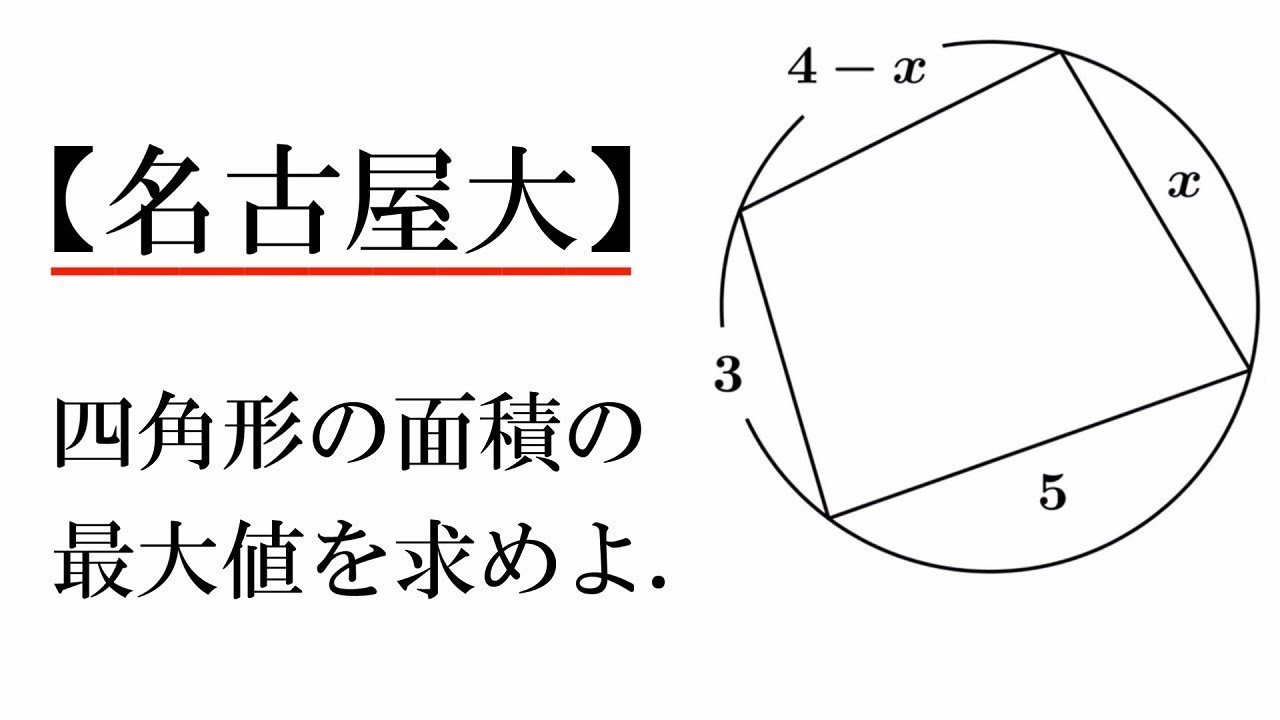



名古屋大 円に内接する四角形と三角比 超わかる 高校数学 A 演習 三角比 26 Youtube




この場合の円に内接する四角形abcdの面積はどのようにして求めるのか教えてください Clear



48s96ub7b0z5f Net Naisetsu Shikakukei



円に内接する四角形の面積 4辺から 高精度計算サイト
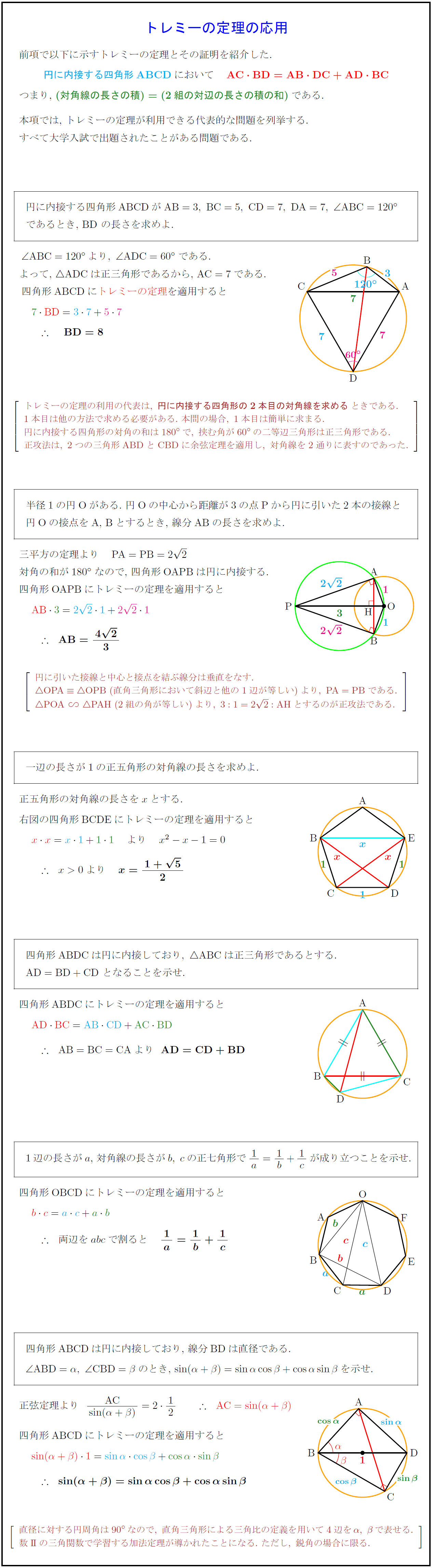



高校数学 トレミーの定理 裏技 の応用6種 円に内接する四角形の対角線の長さなど 受験の月




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
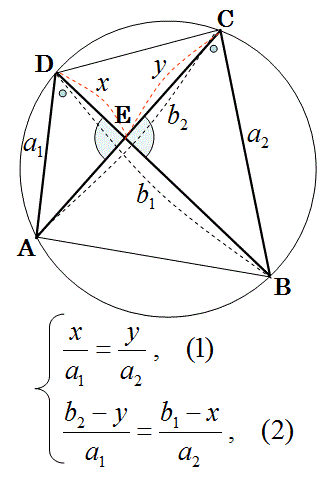



勉強しよう数学 円に内接する四角形の対角線の交差点までの長さ




円に内接する四角形の問題 2019年度前期日程の千葉大学教育学部入試問題 身勝手な主張
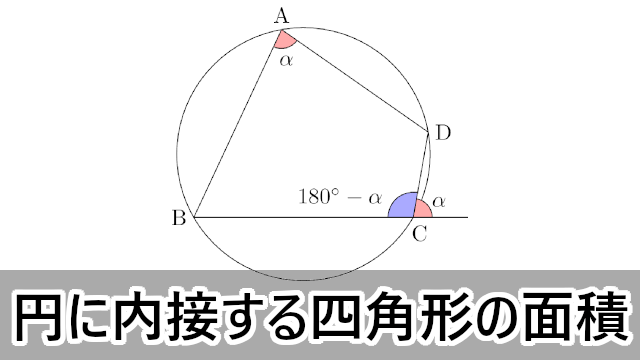



数学ia 円に内接する四角形の面積 大学入試数学の考え方と解法




円に内接する四角形 数学i フリー教材開発コミュニティ Ftext
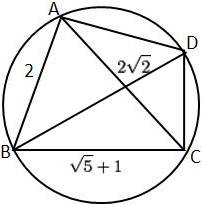



円に内接する四角形 Cdの値の計算 図形 センター数学ia対策過去問題集




円に内接 外接する四角形の性質まとめ 数学の偏差値を上げて合格を目指す



1
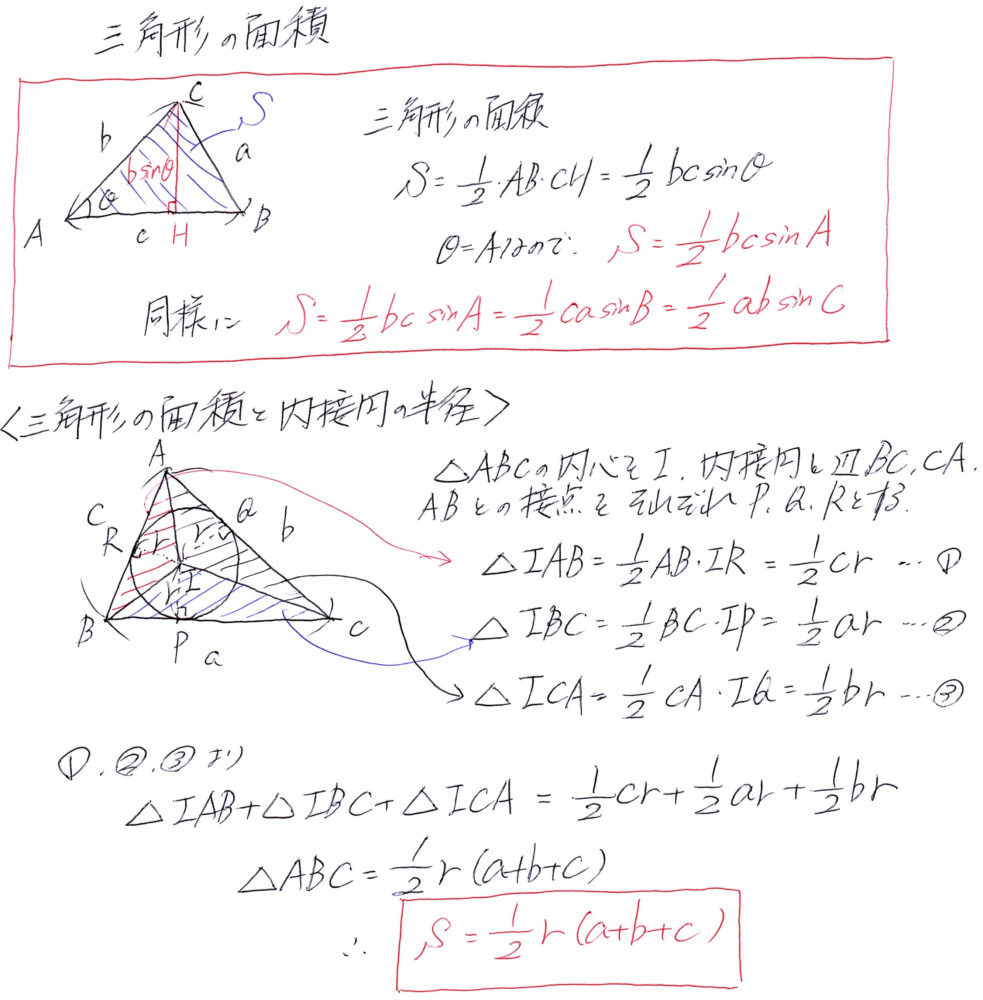



三角形の面積と形状 富岡市の総合学習塾 トータルアカデミー




高校数学 円に内接する四角形の面積ブラーマグプタの公式 裏技 の証明と円に内接しない四角形の面積ブレートシュナイダーの公式 裏技 受験の月



外接円 Wikiwand
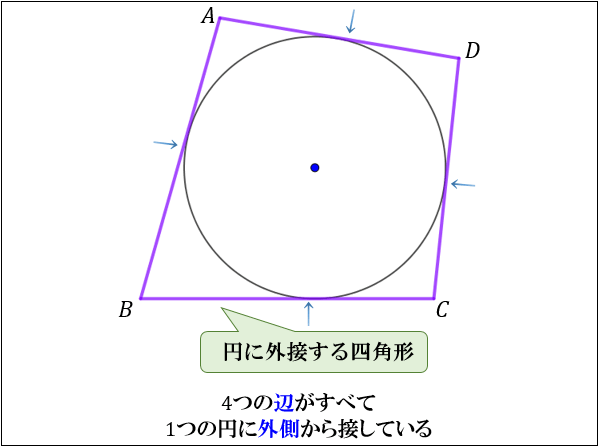



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ



円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する




内接四角形 11年8月2日ブログ問題 カンブリア アカデミー 高等部 Byオルドビスキー博士




円に内接する四角形の問題 問題 円に内接する四角形abcdがあります A Okwave



七五三 三角形から円に内接する四角形へ



Zckzah2254agba360j34p3p4a5h4c Net Category E5 86 86 81 Ab E5 86 85 E6 8e A5 81 99 8b E5 9b 9b E8 92 E5




円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



数学i Aチェック リピート 第4章 2図形への応用 5 円に内接する四角形 Pukiwiki




円に内接する四角形 対角線の線分比の処理 Youtube



Http Www Doutaku Hokkaido C Ed Jp Sankakuhi4 Pdf
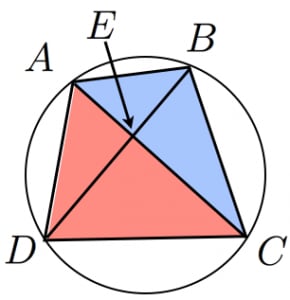



円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語



答1130 円に内接する四角形 解答集



3
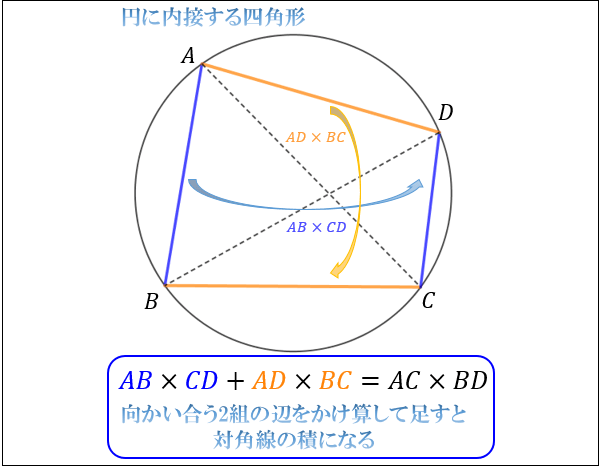



トレミーの定理とその証明 向かい合う2組の辺と対角線の関係性 アタリマエ
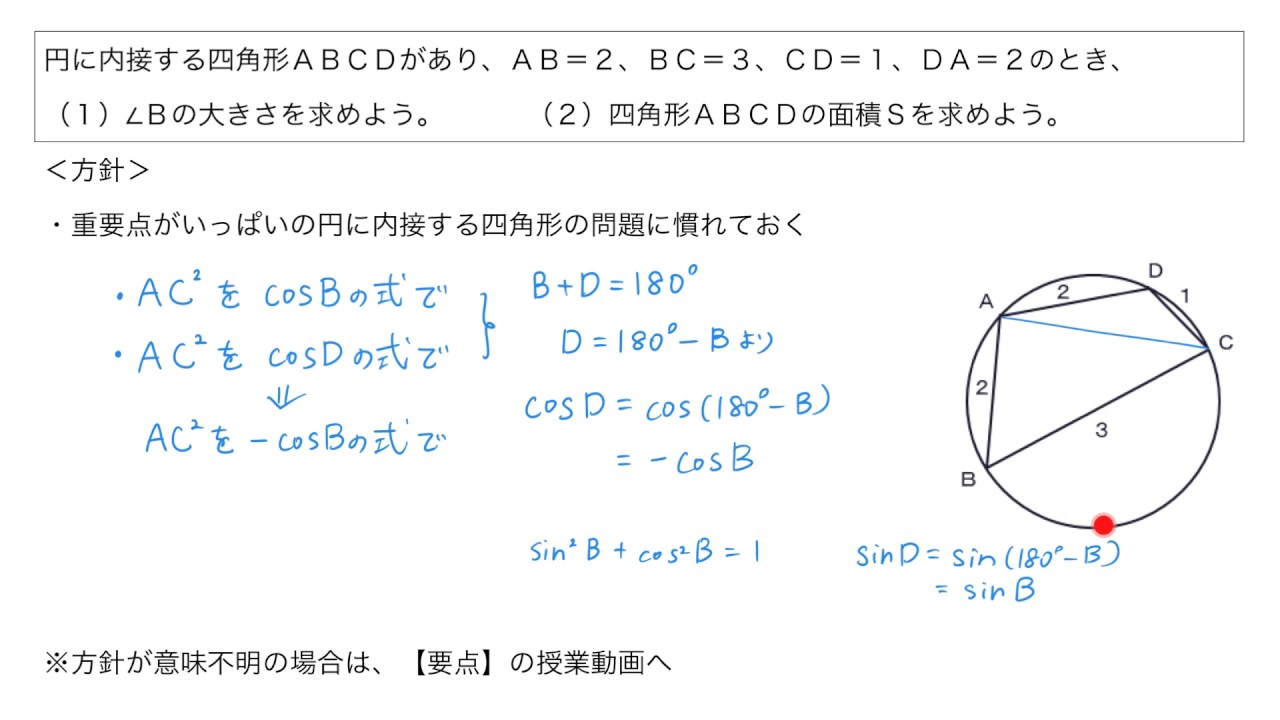



例題 円に内接する四角形 Youtube
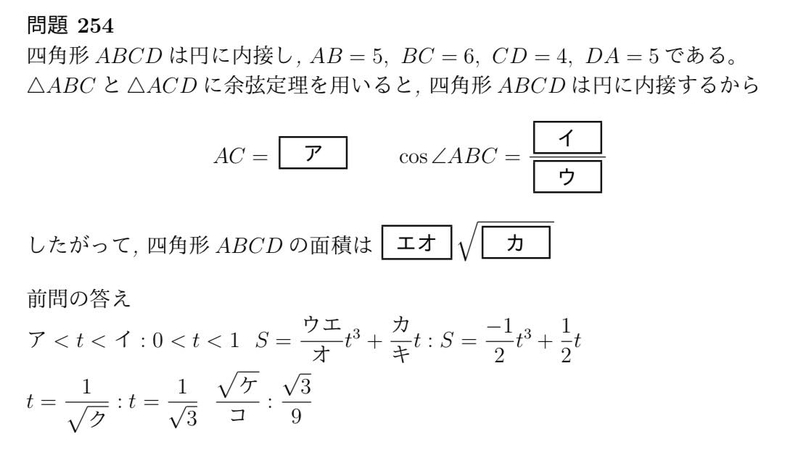



円に内接する四角形の問題ver マーク方式の数学の問題を作ってみた
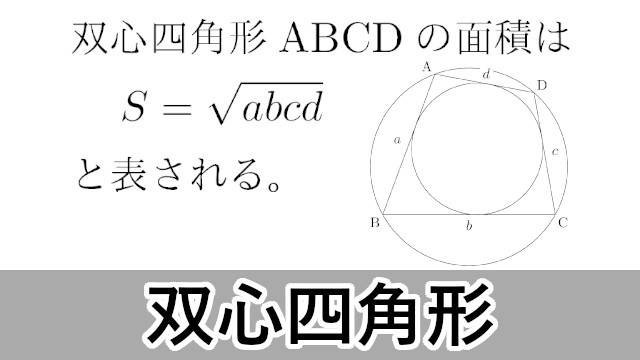



双心四角形の面積 外接円と内接円の両方をもつ四角形 大学入試数学の考え方と解法
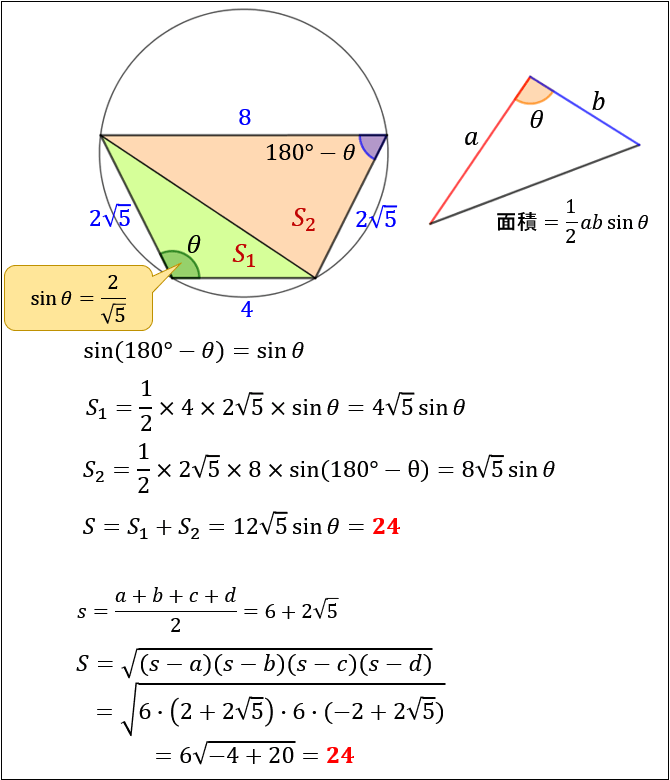



日暮里くん A Twitter ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式




高校数学 数 96 円に内接する四角形 Youtube



七五三 三角形から円に内接する四角形へ



コラム ヘロンの公式 江戸の数学




Ab1 3 Cdda Cosabc Dfra Descubre Como Resolverlo En Qanda




Mondai55




円に内接する四角形の性質 高校数学の知識庫



円に内接する四角形abcdにおいてab 4 3 Cd 2 Da Yahoo 知恵袋



円に内接する四角形 11年センター試験本試数学 A第3問 1 大学受験の王道




サインを使って円に内接する多角形の面積を求める問題 数学i By ふぇるまー マナペディア
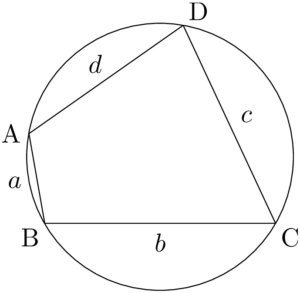



ブラーマグプタの公式 円に内接する四角形の面積 大学入試数学の考え方と解法
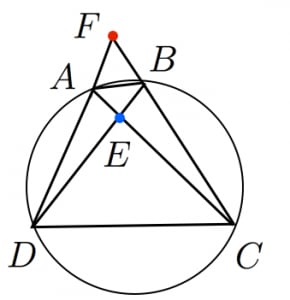



円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語
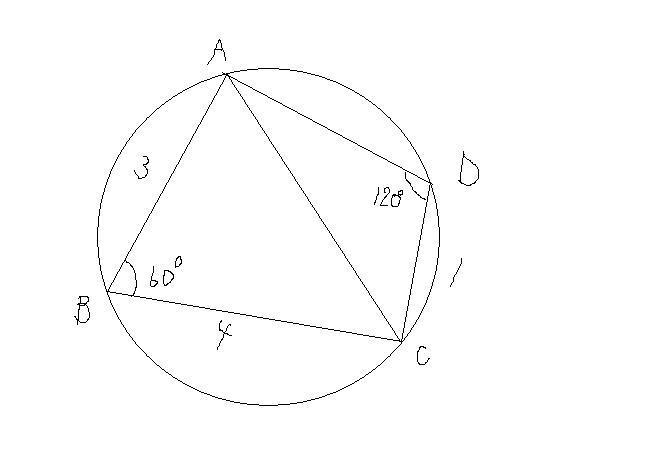



円に内接する四角形の問題です 大学入試数学問題の解説 解答



1
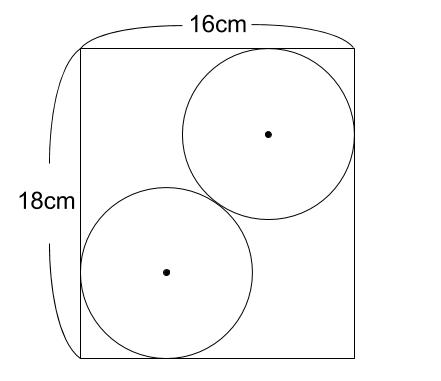



長方形に内接する2つの円 中学数学の無料オンライン学習サイトchu Su




円に内接する四角形 小学5年への説明 再掲 Okwave




円に内接している四角形の面積の最大値について Okwave



趣味の数学問題集 a問題
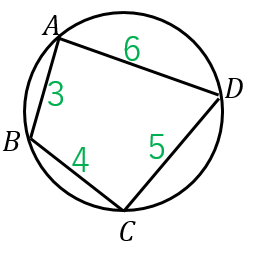



円に内接する四角形の面積を求める公式 具体例で学ぶ数学




Sinb0 Sinbsqrt1 Cos2bsqr Descubre Como Resolverlo En Qanda
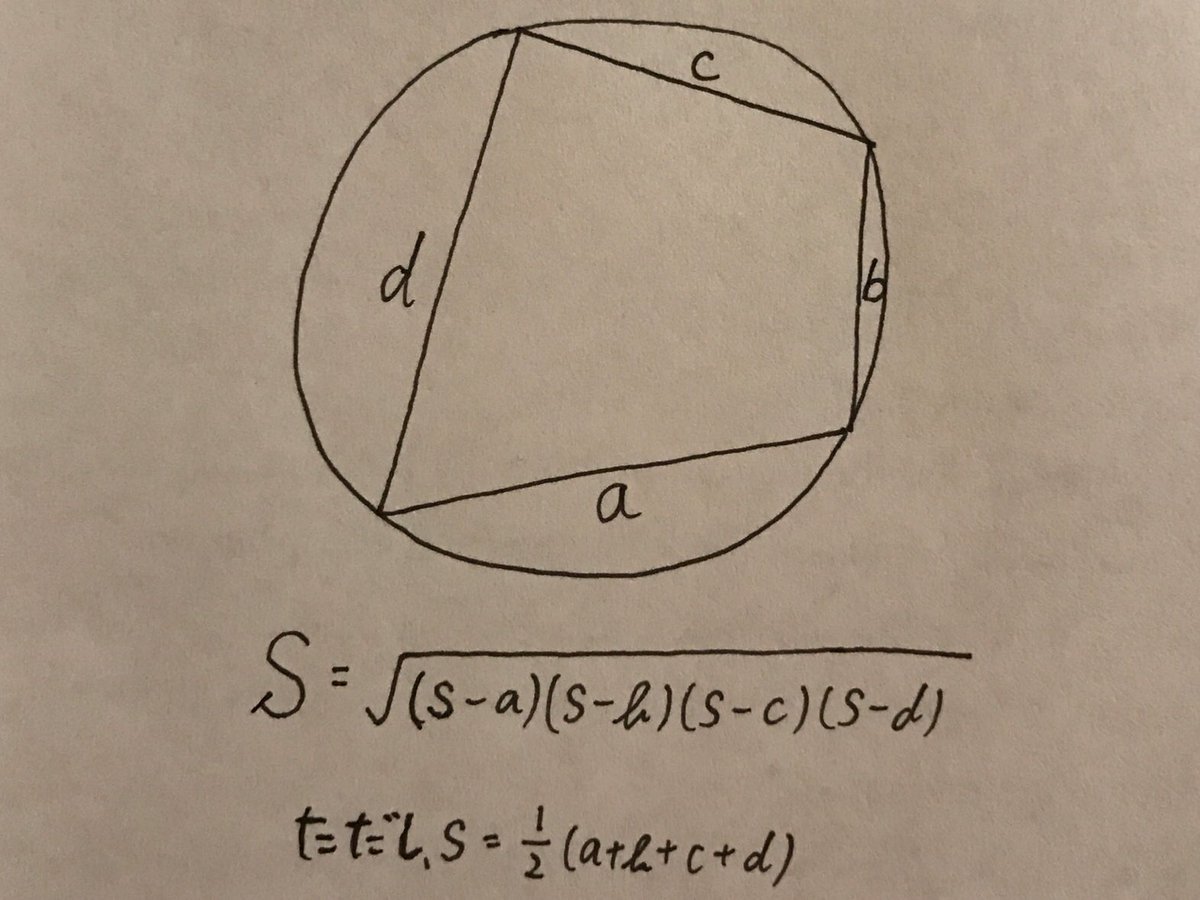



円に内接する四角形の面積sを求めてるなうに使っていいよ Trsene V Twitter




ブラーマグプタの公式 17年 大阪教育大 数学日和



0 件のコメント:
コメントを投稿