√70以上 立体 体積 345205

立体の体積 体積ボタン 解説 体積ボタン2 解説 立体（L字型） 解説 6年 分数のかけ算とわり算 解説 図形・円と直線の関係 解説 比例 解説 比例と反比例① 解説 比例と反比例① v2 解説 比例と反比例② 解説 変化する2つの量 解説 割合を使って こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積（表面積）を求める方法についてまとめています。 前回の記事（Part26）はこちら！ 広義積分・ガウス積分についてまとめています。こ児童の思考の補助をする。本論文では，斜角柱の体積を求める教材の概要について説明し，その 実践のまとめと考察について述べる。 〈キーワード〉立体，斜角柱，等積変形，類推 1 はじめに 本研究の目的は，根拠を明確にして説明する力

小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

立体 体積

立体 体積- 定積分で体積を求める ある曲線下の面積を定積分で求められたように、ある平面を積み重ねてできる立体の体積も、定積分で求められます。 このとき、平面の積み重ね方には大きく分けて次の \(2\) 通りがあります。立体の体積の求め方 これで，円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが，以上の議論は，「任意の立体について，基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば，その立体の体積を定積分により求めることができる。

三角柱とは 体積 表面積の公式や求め方 計算問題 受験辞典

 体積は32π（$cm^3$）となります。 次に、円柱の表面積の求め方は「底面積 × 2 側面積」なので、式は「4π × 2 側面積」。 また、円柱の側面積の求め方は「高さ × 円周」、円周の求め方は「直径 × π」なので、式にすると 4π × 2 8 × 4π = 40π小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題の共通部分 の体積 を求めよ． 次 314 曲面積 上 3 多重積分 前 312 演習問題 ～ 多重積分の積分変数の変換 平成21年12月2日

K 上で定義される関数 z=f (x , y) ≧ 0 について，不等式 0 ≦ z ≦ f (x , y) を満たす xyz 空間の領域（立体）を M とするとき，立体 M の体積を求めることを考える． ※ このように定積分を繰り返し行うこと（累次積分）により重積分の値を求めることができる立体の体積を求めるには，体積の微分が断面積になることを利用します． すなわち，左端 a から座標 x までの区間にある体積を x の関数として V (x) で表し， x における断面積を S (x) とおきます．熊本大学数理科学総合教育センター 3(9)(立体の体積2) 球x 2y z 25 4a2 と円柱x y2 5 a の共通部分E の体積を求めよ． 解 x 2y z2 5 4a 2よりjzj 5 p 4a x2 y2 だから， E = n (x;y;z) x 2y2 5 a ;

〇この立体の体積を求 めましょう。 〇角柱の体積の求め方 で求められないか， 考えてみましょう。 3 見通しをもつ 〇角柱とみるために は，どこを底面にす ればいいのかな。 話し合ってみよう。 4 自力解決をする。 〇公式を使って求めて みましょう。V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S 1 = 角錐底面積 S 2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体回転体の体積 を求める公式 （ただし 0 ≤ α < β 0\leq \alpha

中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー

世界一分かりやすい算数 小６ 立体の体積

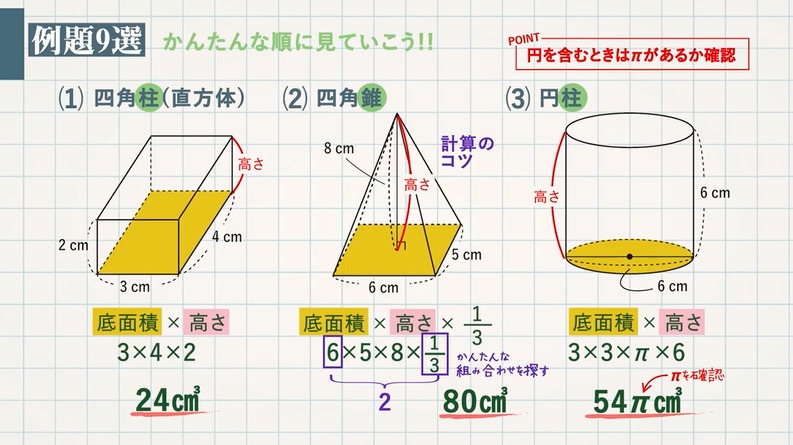
体積 = 底面積 × 高さ柱の体積 = 底面積 × 高さ多面体・正多面体とは まず多面体とは、 複数の平面で囲まれた立体図形 です。 円柱や円錐のように 曲面が含まれる立体は多面体ではありません が、立体を構成する面がどんな図形でもそれが平面なら多面体といいます。 角柱や角錐などは、「多面体」という言い方もあるので複数の名前を

小６算数 立体の体積 は公式が大事 勉強方法 考え方を紹介 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ

スタディピア 立体の体積

‎「立体学習あぷり Lite」のレビューをチェック、カスタマー評価を比較、スクリーンショットと詳細情報を確認することができます。「立体学習あぷり Lite」をダウンロードしてiPhone、iPad、iPod touchでお楽しみください。1 単元名「立体の体積」 2 指導観 本学級の児童（男子19 名、女子9名）は、不えられた計算問題などの課題には一生懸命に取り組むことがで きる。全体的に見ると、習熟度に大きく差が付いており、個別に支援が必要な児童が数名いるため、年度当初よラーニングリソーシズ 算数教材 透明立体図形 14個入り ler4331 正規品がはめこみ・形合わせストアでいつでもお買い得。当日お急ぎ便対象商品は、当日お届け可能です。アマゾン配送商品は、通常配送無料（一部除く）。

Q Tbn And9gcqbxowgsr9fglz9s6nk3xfp1u T2gn5wllytdkpbbfnrgtv43gf Usqp Cau

体積の求め方 計算公式一覧

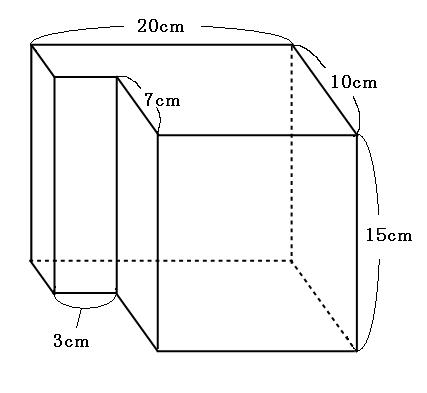
立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も（A）のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答直方体の体積＝縦×横×高さで計算します。 立方体は全ての辺の長さが等しいので、立方体の1辺をaとするとき 立方体の体積＝a×a×a＝a 3 中学生でもおぼえられる「球の体積の求め方」 を解説していくよ。 球の体積の公式を忘れちゃったときに参考にしてみて。 球の体積の公式を1発で覚える方法 「球の体積の公式」を暗記する方法を伝授しよう。 3分の4 × 円周率 × 半径の三乗

Pin On Matematicas

私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館

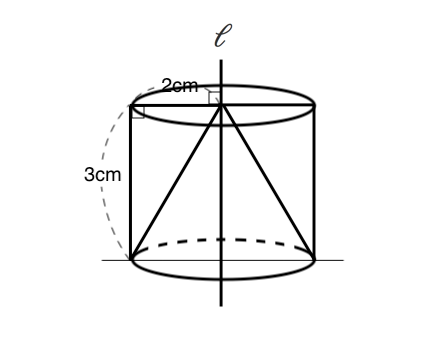
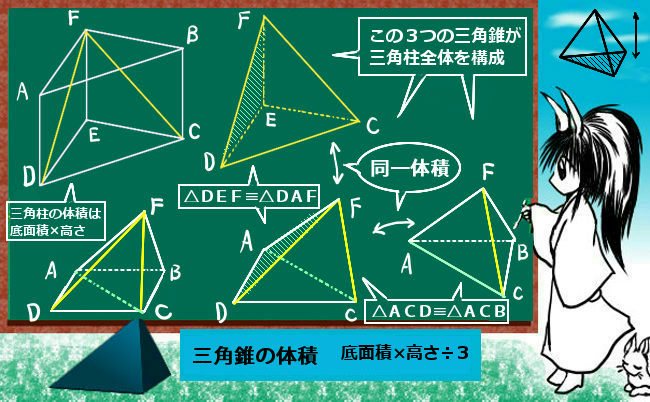
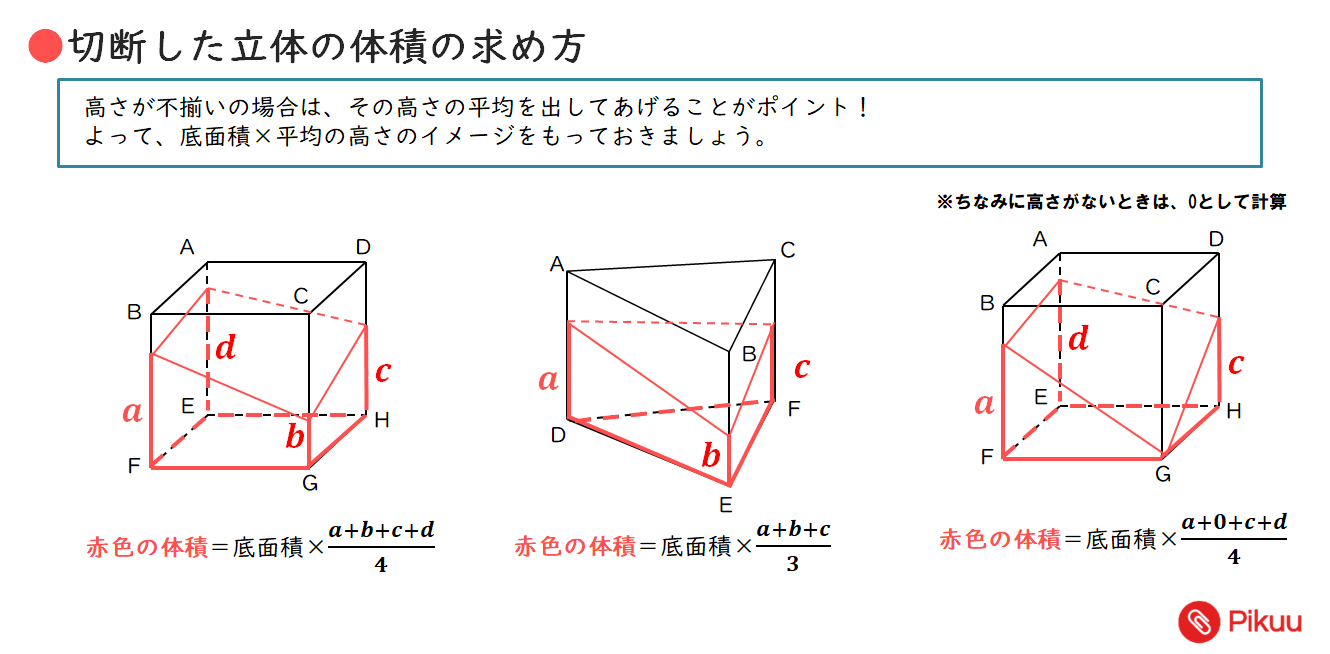
 問題）体積は？ 立体図形を斜めに切断した時の体積は底面積×高さの平均 答え）80cm 3 以上、基本問題でした。5年生の段階では、基本問題を「完璧」に 解ける事が大事です。 まとめ 立体図形を斜めに切断した時の体積は底面積×高さの平均Jzj 5 p 4a2 x2 y o と表される．ゆえに， Vol(E) = ZZZ E dxdydz = ZZ fx2y25a 2g dxdy 図2のように、辺BE上に点Pをとる。三角錐ABCPの体積が三角柱ABCDEFの体積の \(\frac{1}{4}\) 倍であるとき、線分BPの長さは何cmか。 問題4）図3の図形を、直線ℓを回転の軸として1回転させてできる立体の体積を求めよ。 問3）13本 264㎤ 36cm

Studydoctor立体の体積の求め方と公式 柱体 中学１年数学 Studydoctor

角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun

6年算数 立体の体積 その1 子どもの学習支援 by いっちに算数 スマホ版 立方体 直方体 6年生は、上の図のように5年生で勉強した「直方体や立方体」の体積の求め方を生かして、下の図のような「三角柱などの角柱や円柱」の体積の求め方を勉強します。＜ドーナツの体積＞ さて，いよいよ本題に入りましょう。ドーナツ形は下の図のように，円を直線のまわりに1回転させてでき た立体と考えることができます(数学の世界では，円 えん 環 かん 体 たい またはトーラスと呼ばれています）。四角錐台の体積 110 /191件 表示件数 5 10 30 50 100 0 1 10 女 / 40歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 建築設計の折り上げ天井の空調気積と平均天井高さ ご意見・ご感想 計算式も提示頂いてるので、根拠を示せるので助かり

中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clear

立体の体積を求める問題 回転させてできる立体 苦手な数学を簡単に

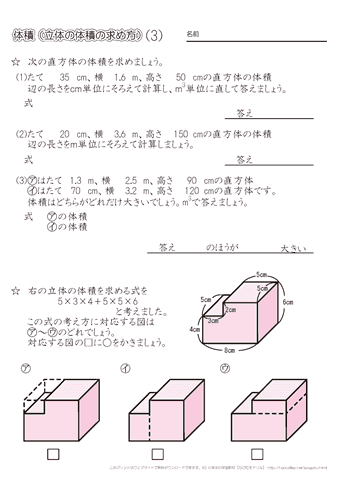
 答え）体積26 cm 3 表面積cm 2 積み重ねられた立体の表面積：（前＋右＋上）×2 積み重ねられた立体①：表面積と体積！ 答え）体積640cm 3 表面積480cm 2 上記のようにある程度、自分の頭で「投影図→見取り図」が2 次の直方体や立方体の体積を求めましょう。 ⑴ ⑵ ⑴答え ⑵答え 3 1辺が6㎝の立方体があります。この立方体と同じ体積で，たて3㎝，横9㎝ の直方体の高さは何㎝ですか。 答え 4 次の展開図を組み立ててできる立体の体積を求めましょう。体積の公式を使って、問題を解くこ とができる。 色々な立体の体積を底面積×高さの公式を 使って求める。 *立体の体積の求め方を説明する。 5 体積の公式を使って適用題を解き、 理解を深める。 「たしかめ道場」の問題を解く。

3 1 Descubre Como Resolverlo En Qanda

小5 複雑な立体の体積 直方体 日本語版 Youtube

その立体の中にどれほどの量の水（あるいは空気や砂など）が入るのかを示す量と考えても良いかもしれません。 体積には立方センチメートル（cm 3 ）、立方メートル （m 3 ）、立方インチ（in 3 ）、立方フィート（ft 3 ）などが一般的に用いられています。行列式と体積 3 次正方行列a の行列式は各列ベクトルの作る立体の体積の絶対値に等しいことを説明した また, 各行ベクトルの作る立体の体積にも等しいことが示される(証明は教科書) a=この立体の体積は (cm 3 ) 外側の体積 160π (cm3)から空洞になっている内側の体積 40π (cm3)を引くと V=1π (cm3) 大きな円錐の体積は π×6 2 ×10÷3=1π (cm3) 上端の円錐の底面の半径 ( x とおく)は，比例（相似）の関係を使って求めることができる．縦：横 x 5x=106

下の図の円すいと円柱を合わせた立体の体積を求めなさい なお 円周率はpを用いる Yahoo 知恵袋

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

空間図形 (発展) 図は一辺12㎝の立方体である。 AP=3㎝、BQ=7㎝とする。 D,P,Qを通る平面でこの立方体を切ったときの切り口をDPQSとする。 (1) CS の長さを求めよ。 (2) 切断してできる立体のうち頂点Bを含むほうの立体の体積を求めよ。 図のような1辺6cmの立方47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ，円柱とその展開図である。 次の問いに答えよ。 正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。

５ ８ 円柱を３等分した図形の体積と面積を求めるには さんすうがく

小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

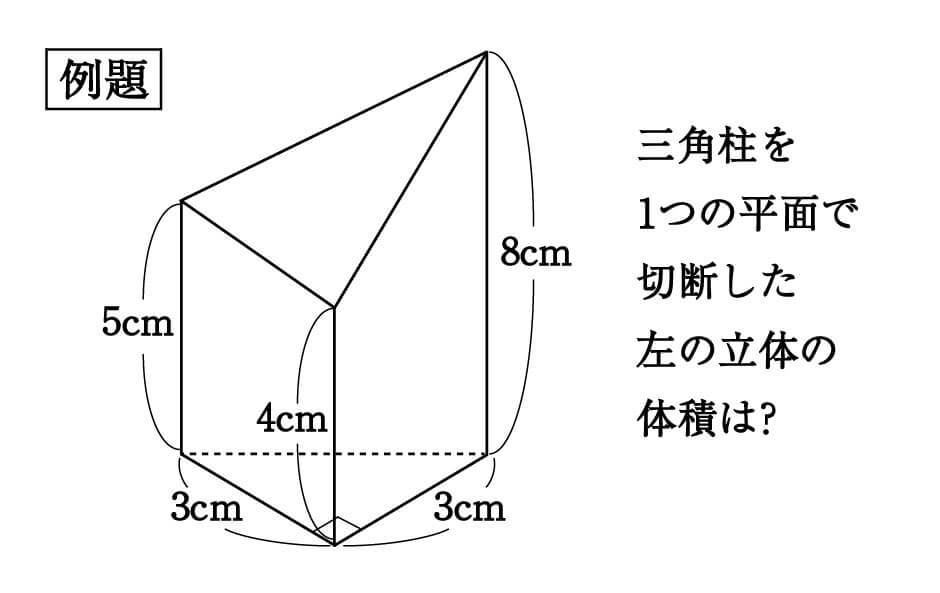
数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三角柱とは 体積 表面積の公式や求め方 計算問題 受験辞典

小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

立体の表面積と体積 数学の要点まとめ 練習問題一覧

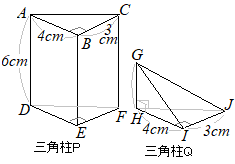
立体の体積

体積の求め方 計算公式一覧

複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学

点dを含む立体の体積は 今年 ２０１８年 芝中学 どう解く 中学受験算数

Math ややこしい立体の体積は 柱と錐に分割して求める 働きアリ

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

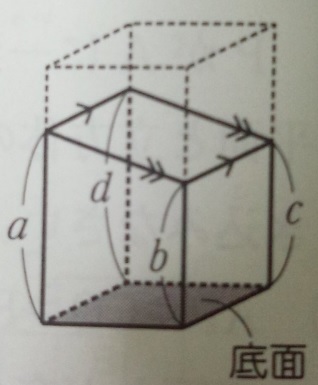
立体図形を斜めに切断した時の体積は 底面積 高さの平均 中学受験 塾なし の勉強法

算数プリント６年生 立体の体積 角柱 円柱

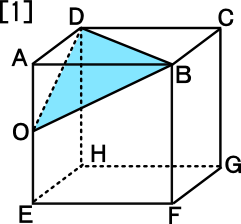
中学１年数学練習問題 切り取った立体の体積の求め方と解答

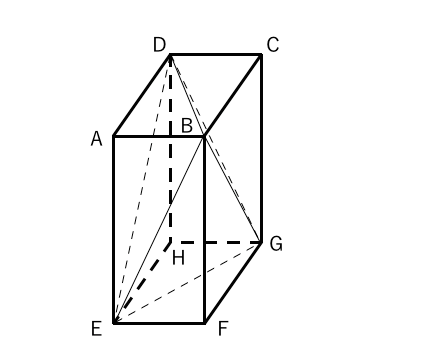
毎日問題を解こう 18 苦手な数学を簡単に

くりぬき立体の切断 体積 Geogebra

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ

不等式で表された立体の体積 02年 大阪府大 大学入試数学の考え方と解法

立体の体積 理数系無料オンライン学習 Kori

中1数学 立体の体積 例題編 映像授業のtry It トライイット

６年算数立体の体積１ 教え方

Math ややこしい立体の体積は 柱と錐に分割して求める 働きアリ

立体の体積の求め方 何角柱でも何角錐でも同じ

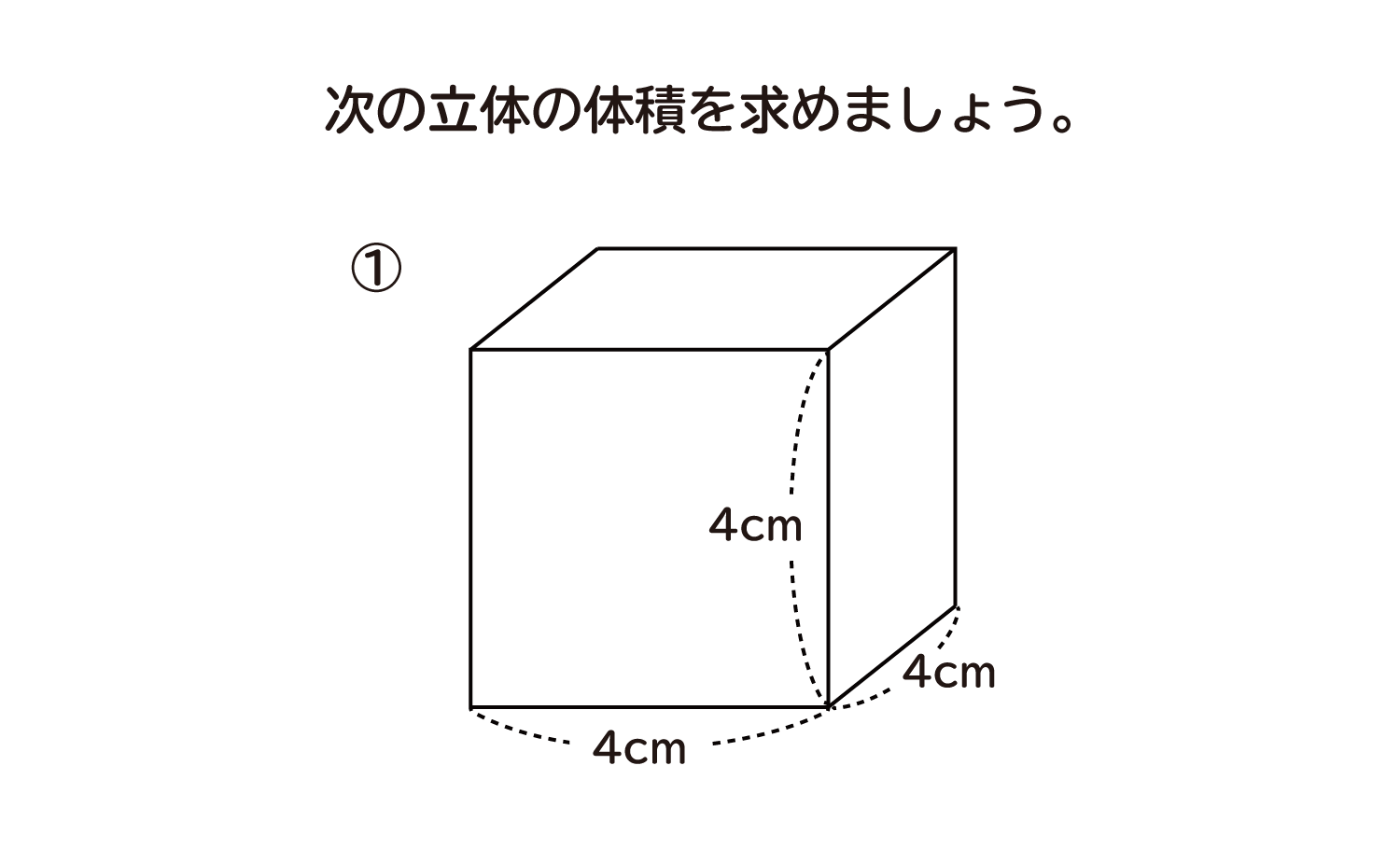
小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル

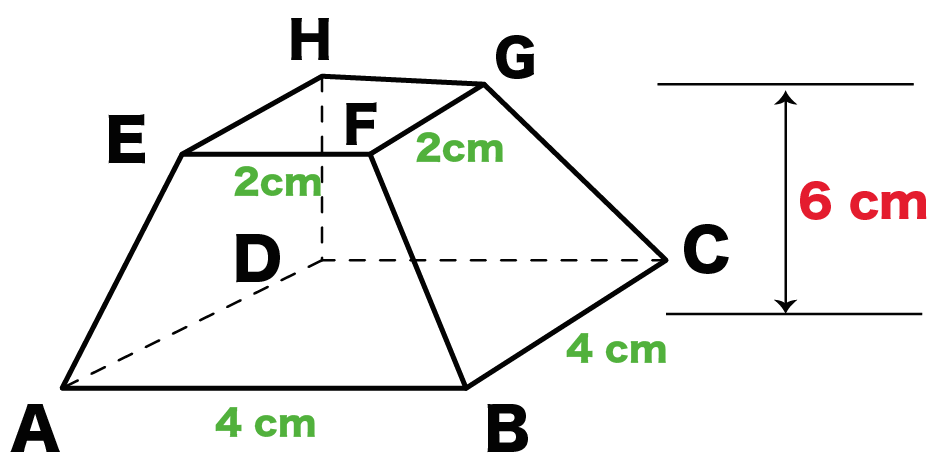
簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題

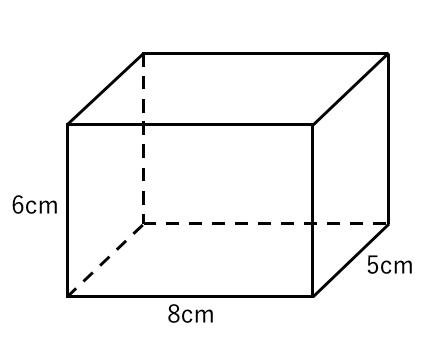
立体の体積を求める 苦手な数学を簡単に

体積の求め方 計算公式一覧

小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

体積の求め方 公式一覧 小学生 中学生の勉強

円錐の体積ってなんであの公式なの Webty Staff Blog

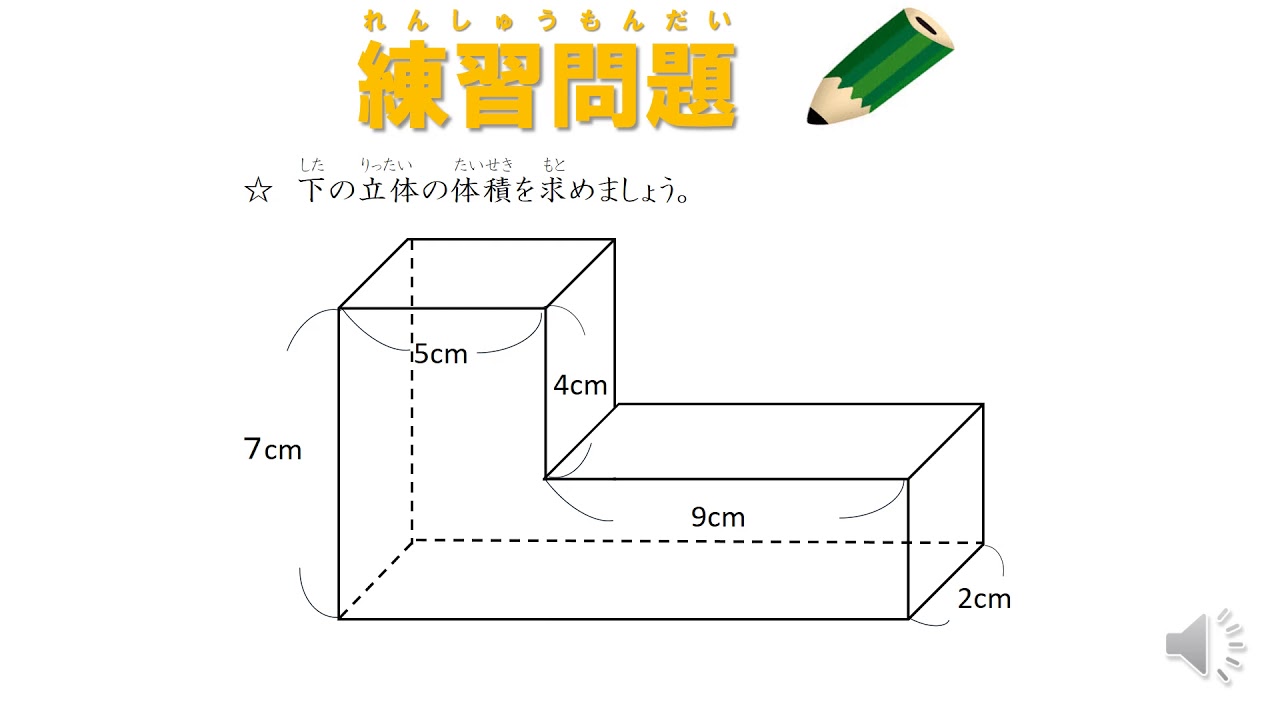
小5 直方体の体積 複雑な立体を求める 日本語版 Youtube

中1 数学 中1 立体の体積 Youtube

角錐 円錐の体積と表面積の公式 数学fun

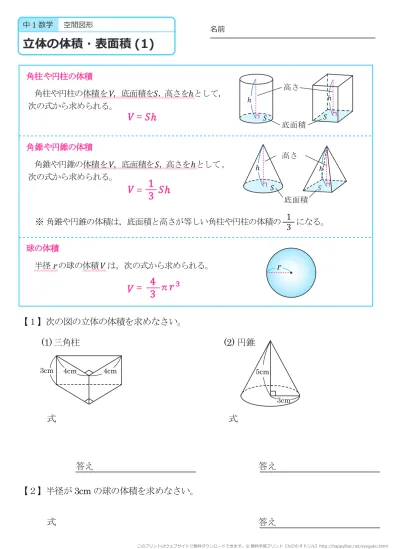
中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 このページの問題プリント 全部

無料 中１数学 基本解説 問題プリント 空間図形５ 立体の体積 143

小6 算数 立体の体積 小学生 算数のノート Clear

算数 数学の知っておくと便利なお話 立体図形編 ｓｔ 14 スタディ教室長の教室通信

世界一分かりやすい算数 小６ 立体の体積

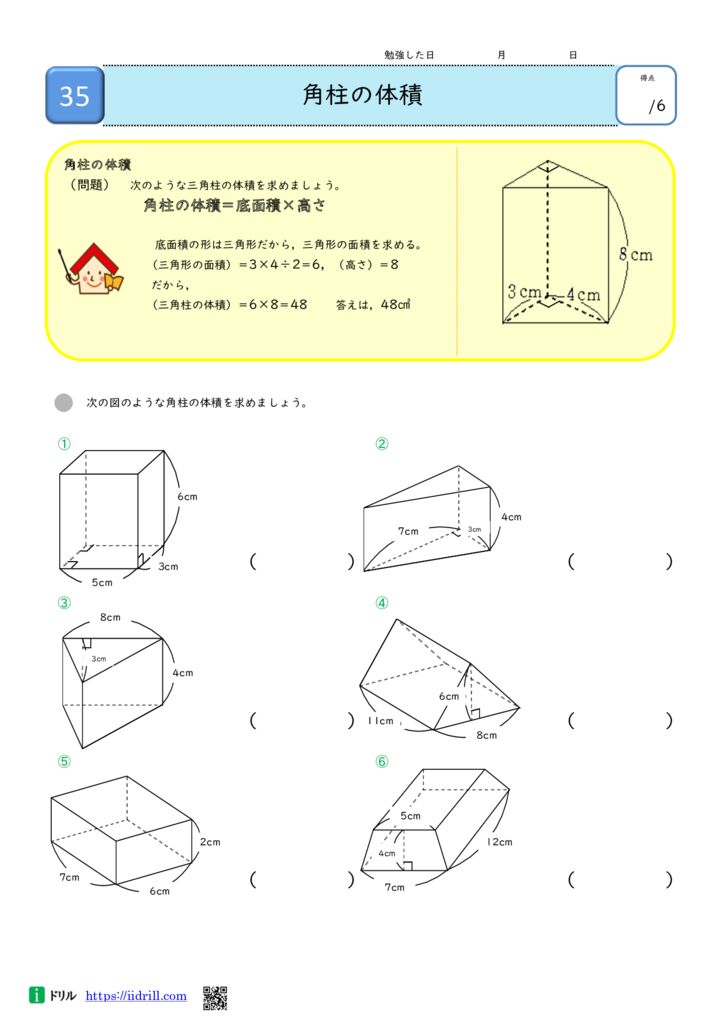
6年生算数ドリル 立体

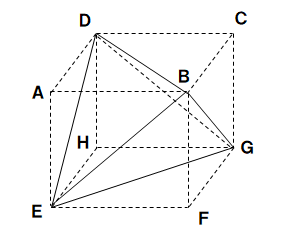
中1数学 立体の表面積と体積の求め方と練習問題 Pikuu

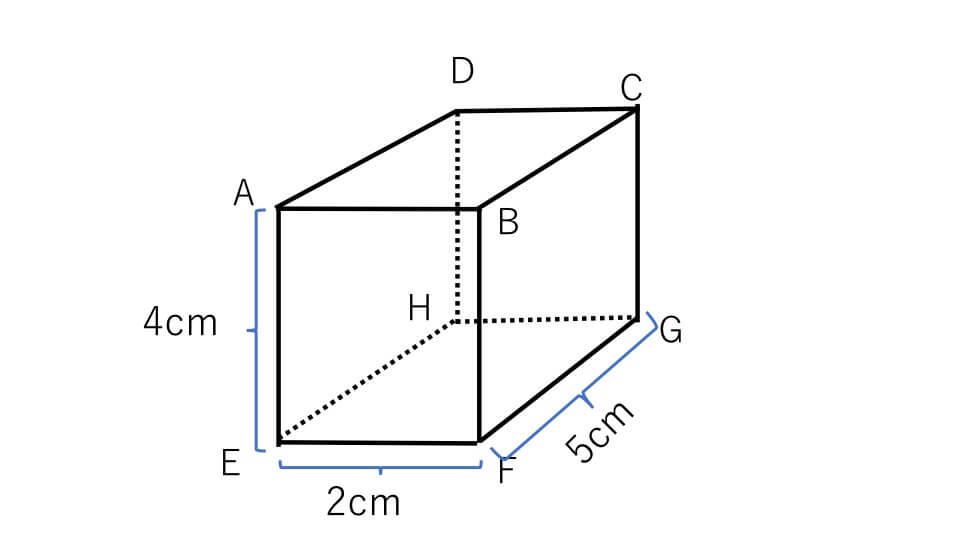
中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー

立体の体積 無料で使える中学学習プリント

６年算数立体の体積その２ 教え方

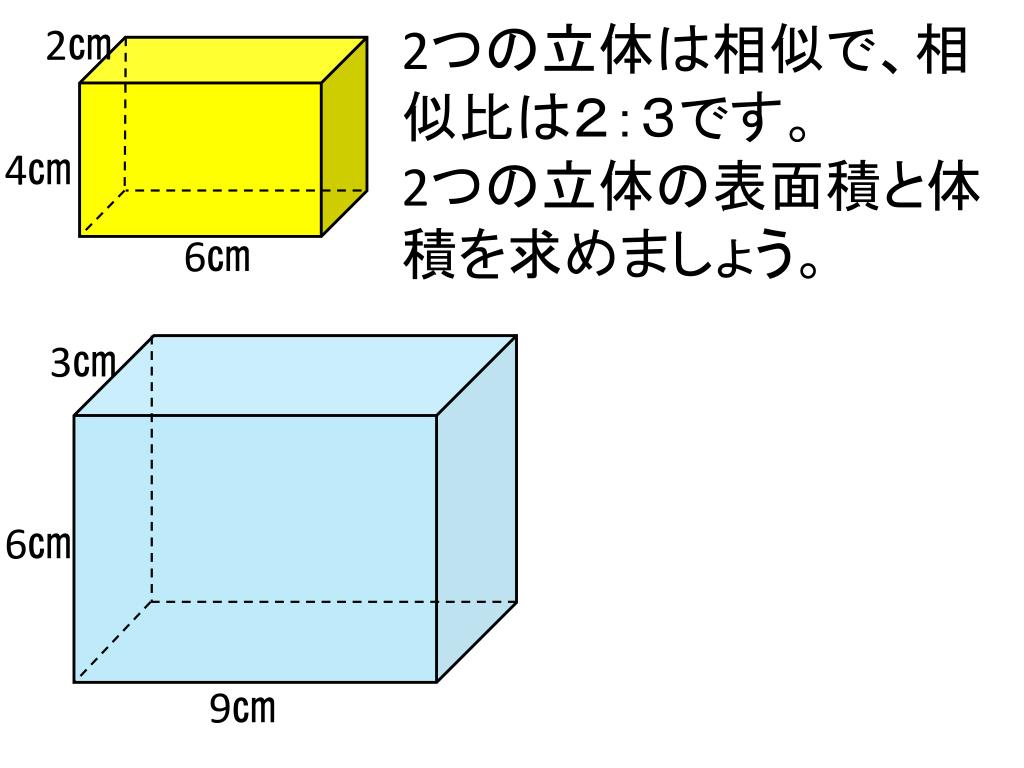
Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

立体図形の体積と表面積 学ぶ 教える ｃｏｍ

1

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト

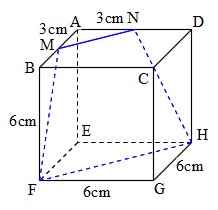
Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ

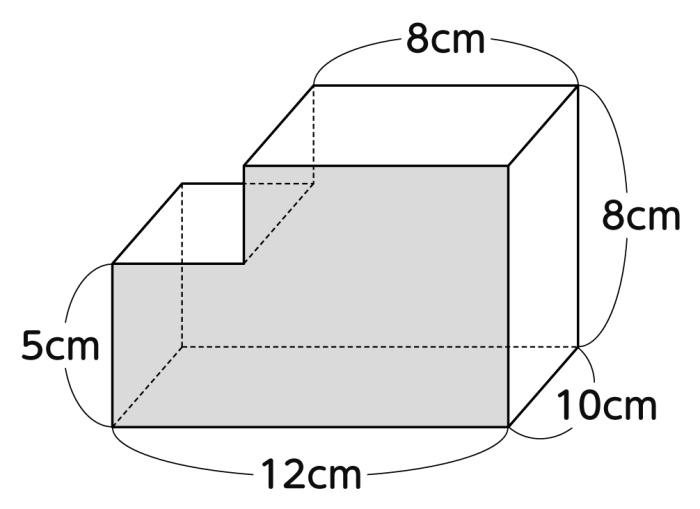
動画で学習 1 角柱と円柱の体積 算数

立体の体積1 Geogebra

立体の体積問題 12年 麻布中学校 恋する中高一貫校 適性検査 徹底攻略

中3 三角形の相似 円錐の体積比 日本語版 Youtube

円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学

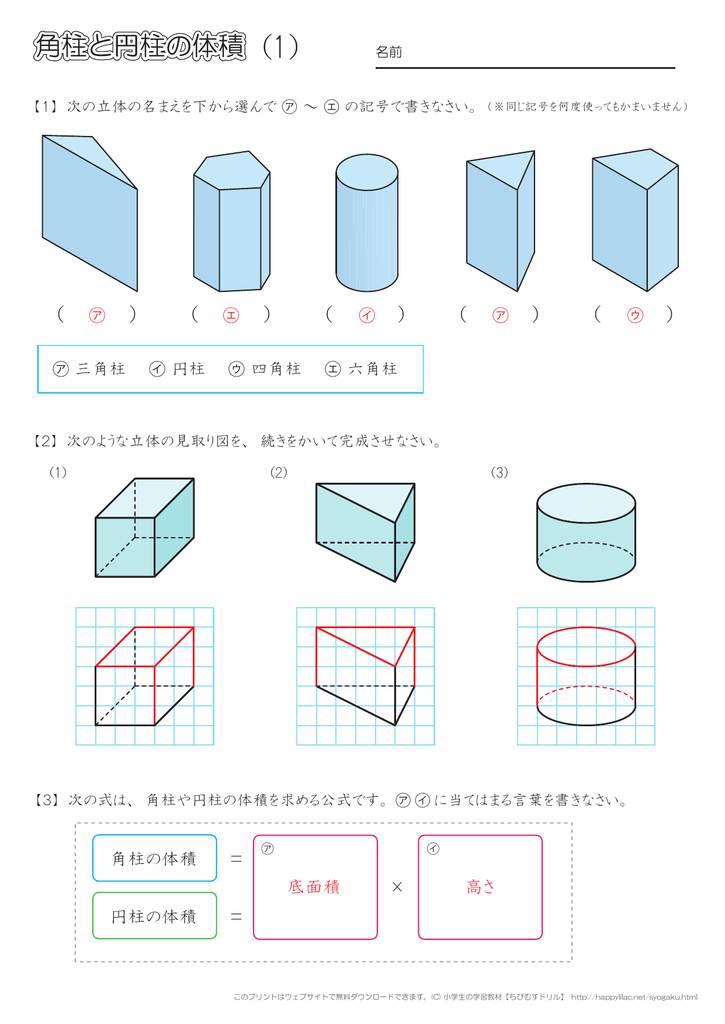
角柱と円柱の体積

高校入試 英語 数学 学習 立体の表面積と体積

体積について 小学校算数 中学校数学から 身勝手な主張

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

すぐるゼミ 立体の切断２

中1数学 立体の体積 練習編 映像授業のtry It トライイット

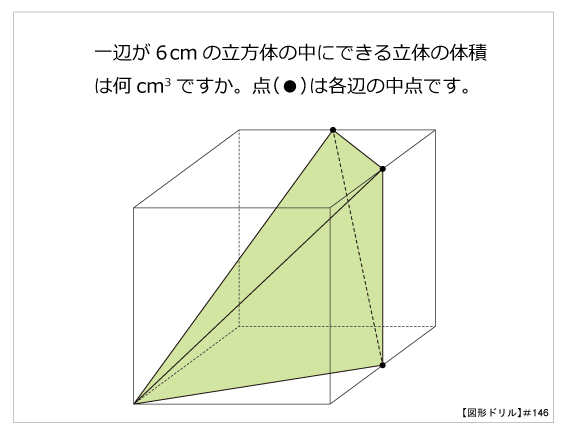
図形ドリル 第146問 立体の体積 算数星人のweb問題集 中学受験算数の問題に挑戦

立体の体積 無料で使える中学学習プリント

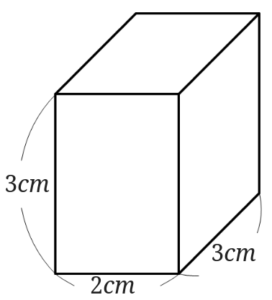
直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校

体積比の求め方が分かりません Clear

６年算数立体の体積その２ 教え方

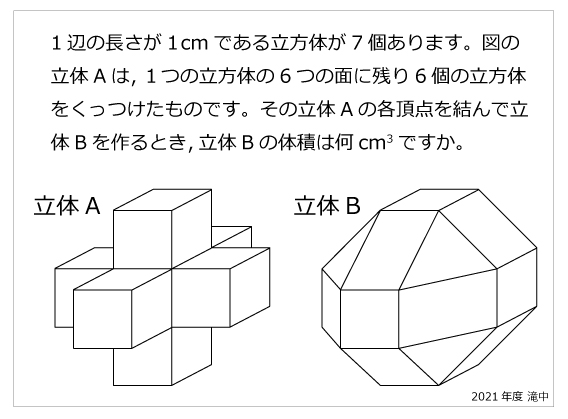
今年の1問 21年滝中 立体の体積 算数星人のweb問題集 中学受験算数の問題に挑戦

スタディピア 立体の体積

立体の体積 テストの前に

体積の測定 測定のことを 即 知りたい ソクシリ キーエンス

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学

1

四角錐 円錐の体積 チーム エン

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

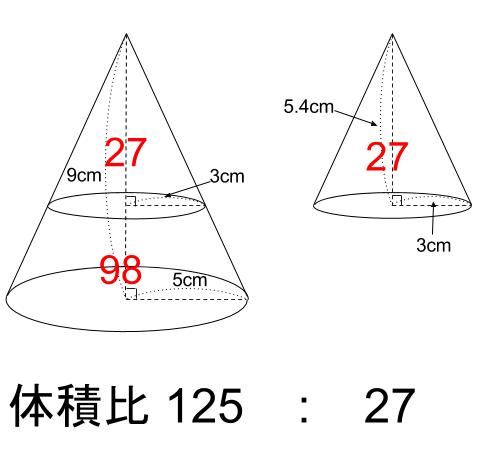
中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su

立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun

中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ

1

立体の体積を求める公式

小６算数 立体の体積 は公式が大事 勉強方法 考え方を紹介 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ

高校入試対策数学 切断した立体の体積を求める練習問題 Pikuu

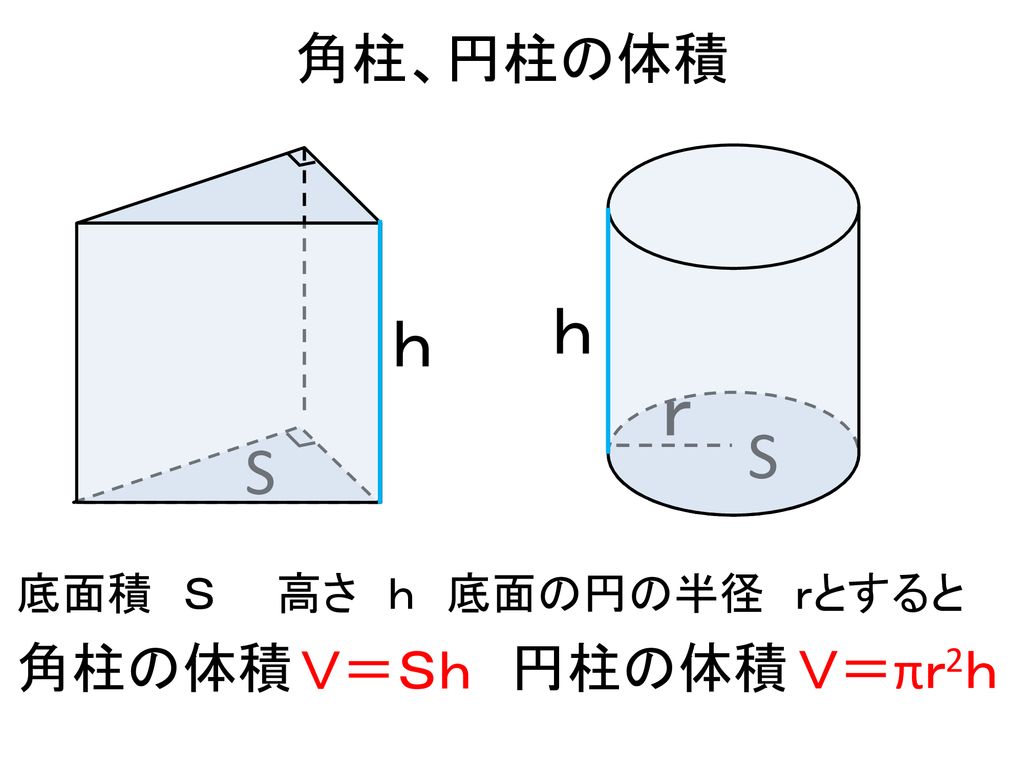
本時の目標 いろいろな立体の体積を求めることができる Ppt Download

この立体の体積は ２０１５年 成城学園中学 これが中学入試に出た図形問題

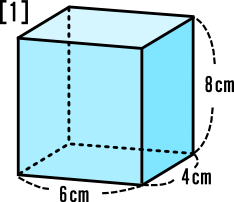
中学１年数学練習問題 立体 円柱 三角錘 四角錘等 の体積の問題