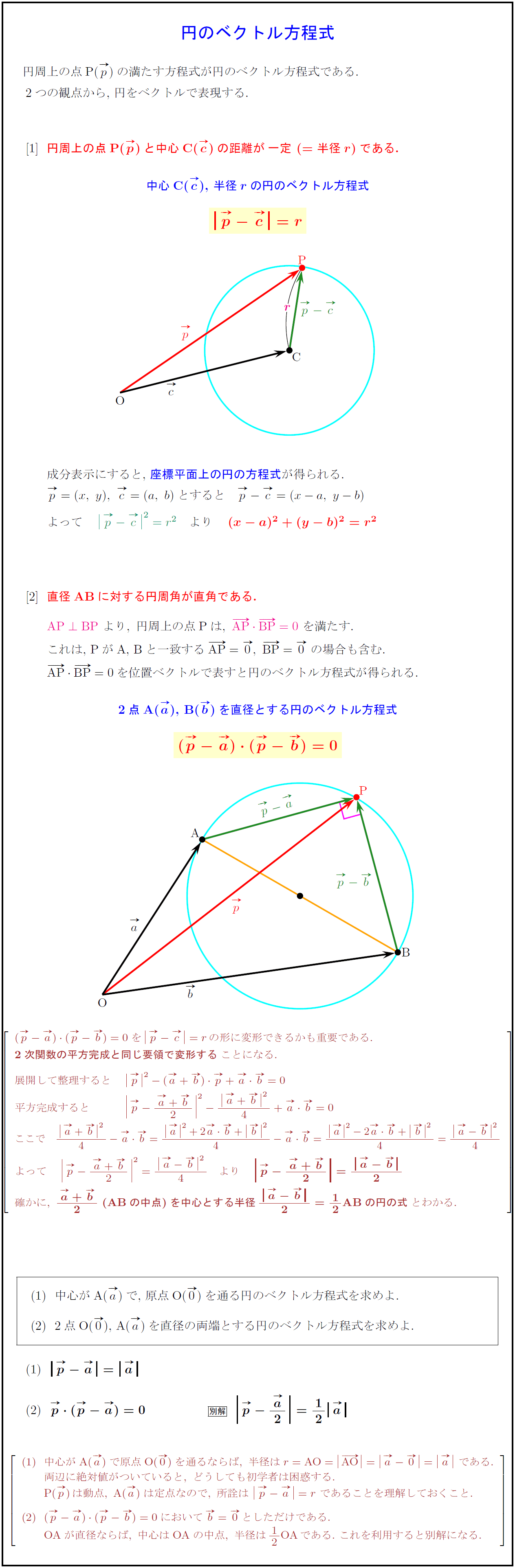
几何课关于三角形你不得不记住的定理：从勾股定理到托勒密定理 直角三角形的两条直角边的平方和等于斜边的平方。 也叫毕达哥拉斯定理。 表达式为a b =c 。 在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。 也叫欧几里德定理。 在RtABC中，∠ACB=90°，CD是斜边AB上的高，则有座標上での2点間の 三平方の定理とは、直角三角形の三辺の長さに関する定理である。 斜辺の2乗は他の2辺の2乗の和に等しくなる。 三角形の三辺をa,b,cとし、斜辺がcとするとc^2=a^2b^2となる。左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64
三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典
数学Ⅱ（図形と方程式）：円の方程式 ①（基本形） 対象 高校生 再生時間 318 説明文・要約 ・円上の点 (x, y)：中心 (a, b) からの距離が一定（＝半径） ・xy平面上の距離：三平方の定理を利用 → (x－a) 2 ＋ (y－b) 2 ＝r 2 が得られる 関連動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 中学数学 平面図形 円と三角形の証明 （1）三角形abg $\equiv$ 三角形dbeであることを証明せよ。 （2）ab＝10cm, be=3cm, cg=5cm のとき、線分bfの長さを求めよ。 解答 円と三角形の証明 （1） 中学数学 平面図形 円と三角形の証明 解答1 三角形abgと三角形dbeにおいて ba＝bd (仮定)・・・① 角bag＝角bde
高校数学b 円のベクトル方程式2パターン 受験の月
三角形の内接円・外接円の書き方を解説！←今回の記事 直角を三等分する線の作図方法とは 回転移動の中心を求める方法とは？作図の方法を解説！ 最短距離にするためにはどこを通る？？ 平行四辺形の書き方、コンパスを使って作図する方法は？Jan 11, 21 · 球体を描いて保存する Powerpoint16 初心者のためのoffice講座 18年東京都公立高校入試の前期大問2立体図形の問題と解説 カンタン作図 円柱の展開図の書き方がわかる3つのステップ Qikeru 平面から立体の半球を製作可能な展開図 球体の展開図 気ままに起承転々天 中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su おさいほう 球や半円の型紙のX = − b ax = \dfrac {b} {a} x = −ab $$ x = \dfrac {b} {a} $$
円と球 どうすればお宝の場所がわかるだろうか 館山市立北条小学校 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
要使用 查找相似位置 工具，您需要提供参考位置、候选搜索位置和表示匹配条件的字段。针对分析选择的图层应包含参考位置或基准 位置。例如，参考位置可能是包含绩效最佳的商店或遭受最严重疾病的村庄所在的图层。然后指定包含候选搜索位置的图层。这可能是所有商店或所有其他村庄。最后A・相似な三角形を自力で3通り作図できる。 B・相似な三角形をヒントを手がかりに3通り作図することが できる。 知識・理解 A・なぜ相似の関係となるかを定義を使って説明した記述があ る。 B・相似であるかどうかを判定できる。 6 単元指導計画(b) 相似変換は角度を保つので原点での角は 等式 㲃10(zw) = 㲃10z 㲃10w をみたす．!
5章1節11 相似の証明の書き方 2組の角 中村 翔
教師支援アプリ！ 中学数学の平面図形を、自由に傾きなどを変化させて直感的に分かりやすく表示できます。 特徴 ・使用が簡単 iPhoneかiPadに表示させて、教室のテレビやスクリーンに映すだけ。面倒な電子黒板の準備や移動教室は不要です。 ・並行移動や回転移動を動的に見せることが岡山大学算数・数学教育学会誌 『パピルスj第23 号(却16 年)69頁72頁 小学算数「図形の合同Jにおける教科書比較 富永雅*角野兼太郎帥 出来光夫*帥 r一一一一一一一一一一一一一一一一一一一研究の要約 j 小学校算数第5学年で学習する「図形の合同Jにおいて、各教科書を精査し、学習指導要領と 塾で習った範囲までをまとめてみました ︎📖 なぜか数学のノートは初めてです🔅 年級 Junior High2, 單元 平行線と角,合同な図形と証明,三角形,四角形, Keyword 中2,数学,図形,証明,合同,三角形,平行四辺形,liese,math
中学数学図形問題の無料プリント ネットレの情報館 楽天ブログ
Amazonでの定期テスト ズバリよくでる 中学1年 数学 啓林館版。アマゾンならポイント還元本が多数。作品ほか、お急ぎ便対象商品は当日お届けも可能。また定期テスト ズバリよくでる 中学1年 数学 啓林館版もアマゾン配送商品なら通常配送無料。 期末テストで数学の成績が下がる原因は？ 1年生1学期の期末テストで数学の成績が下がる原因は大きく2つあります。 計算の正確性 中学校で学習する計算、特に中学1年生で学ぶ内容はそれほど難しくはありません。でも計算手順が多い場合があります。 1 第1学年 1学期期末テスト問題と解答 H29 問題用紙：word10 解答用紙 と模範解答：word10 テスト範囲正負の数、文字を使った式の式の値まで 勤務校平均点 770 H27 問題用紙：word10 解答用紙 ：word10 解答：word10
中１数学 １学期期末テスト対策 予想問題 Youtube
